Question

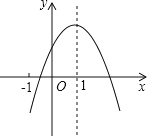
【题目】已知二次函数，当时，恒有；关于的方程的两个实数根的倒数和小于.求的取值范围.

Answer 1

【答案】

【解析】

①y＝x2＋（m＋3）x＋m＋2＝（x＋1）（x＋m＋2），再由当1＜x＜3时，恒有y＜0，可得出m的范围；

②利用根与系数的关系，得出x1＋x2及x1x2的值，根据＜，也可得出m的取值范围，两个范围结合可得出答案．

①由题意可得，方程x2＋（m＋3）x＋m＋2＝0与x轴有两个交点，

故有△＞0，即（m＋3）24（m＋2）＞0，

解得：m≠1，

又因为y＝x2＋（m＋3）x＋m＋2＝（x＋1）（x＋m＋2），

当y＜0时，x可取两个范围：1＜x＜m2或m2＜x＜1，

而由题意得，当1＜x＜3时，恒有y＜0，

故可得，当y＜0时，x的取值范围为：1＜x＜m2，

也可得出m2≥3，

解得：m≤5；

②由题意得，方程x2＋（m＋3）x＋m＋2＝0有实数根，

故有△≥0，即（m＋3）24（m＋2）≥0，

解得：m可取任意实数，

又因为＝＝＜，

解得：m＜12．

综合①②可得：m＜12．