Question

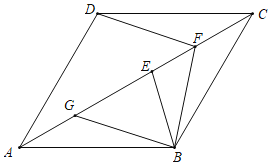
【题目】如图，四边形ABCD为菱形，∠BCD＝60°，E为对角线AC上一点，且AE＝AB，F为CE的中点，接DF、BF，BG⊥BF与AC交于点G；

（1）若AB＝2，求EF的长；

（2）求证：CG﹣EF＝BG．

Answer 1

【答案】（1）﹣1；（2）详见解析．

【解析】

（1）连接BD交AC于O，由菱形的性质得出∠BAD＝∠BCD＝60°，AC⊥BD，OB＝OD，OA＝OC，∠OAB＝∠BAD＝30°，由直角三角形的性质得出OB＝AB＝1，OA＝OB＝，得出AC＝2OA＝2，求出CE＝AC﹣AE＝2﹣2，即可得出答案；

（2）设AB＝2a，同（1）得OB＝AB＝a，OA＝OB＝a，得出AC＝2OA＝2a，求出CE＝AC﹣AE＝（2﹣2）a，OE＝AE﹣OA＝（2﹣）a，得出OF＝OE+EF＝a，得出OB＝OF，证出△BOF是等腰直角三角形，得出∠BFG＝45°，证明△BFG是等腰直角三角形，得出GF＝BG，即可得出结论．

解：（1）连接BD交AC于O，如图所示：

∵四边形ABCD是菱形，

∴∠BAD＝∠BCD＝60°，AC⊥BD，OB＝OD，OA＝OC，∠OAB＝∠BAD＝30°，

∴OB＝AB＝1，OA＝OB＝，

∴AC＝2OA＝2，

∵AE＝AB＝2，

∴CE＝AC﹣AE＝2﹣2，

∵F为CE的中点，

∴EF＝CE＝﹣1；

（2）证明：设AB＝2a，

同（1）得：OB＝AB＝a，OA＝OB＝a，

∴AC＝2OA＝2a，

∵AE＝AB＝2a，

∴CE＝AC﹣AE＝（2﹣2）a，OE＝AE﹣OA＝（2﹣）a，

∵F为CE的中点，

∴EF＝CE＝（﹣1）a，

∴OF＝OE+EF＝（2﹣）a+（﹣1）a＝a，

∴OB＝OF，

∵AC⊥BD，

∴△BOF是等腰直角三角形，

∴∠BFG＝45°，

∵BG⊥BF，

∴△BFG是等腰直角三角形，

∴GF＝BG，

∵GF＝CG﹣CF＝CG﹣EF，

∴CG﹣EF＝BG．