题目内容
15.如图所示,直线AB与反比例函数图象相交于A、B两点,已知A(1,4).(1)求反比例函数的解析式;
(2)连接OA,OB,当△AOB的面积为$\frac{15}{2}$时,求直线AB的解析式.
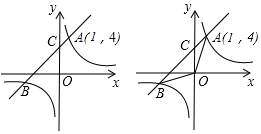
分析 (1)利用待定系数法,即可求出反比例函数解析;
(2)求出反比例函数与一次函数的交点坐标,利用S△AOB=S△AOC+S△BOC求直线AB的解析式.
解答  解:(1)设反比例函数解析式为y=$\frac{k}{x}$,
解:(1)设反比例函数解析式为y=$\frac{k}{x}$,
∵点A(1,4)在反比例函数的图象上
∴k=1×4=4,
∴反比例函数的解析式为y=$\frac{4}{x}$.
(2)设直线AB的解析式为y=ax+b(a>0,b>0),则当x=1时,a+b=4,即b=4-a.
由$\left\{\begin{array}{l}{y=\frac{4}{x}}\\{y=ax+b}\end{array}\right.$可得ax2+bx-4=0,
即ax2+(4-a)x-4=0,
∴(x-1)(ax+4)=0,
解得x1=1,x2=-$\frac{4}{a}$,
设直线AB交y轴于点C,则C(0,b),即C(0,4-a),
∵S△AOB=S△AOC+S△BOC=$\frac{1}{2}$(4-a)×1+$\frac{1}{2}$(4-a)×$\frac{4}{a}$=$\frac{15}{2}$,
整理得a2+15a-16=0,
∴a=1或a=-16(舍去),
∴b=4-1=3,
∴直线AB的解析式为y=x+3.
点评 本题主要考查了反比例函数与一次函数的交点问题,解题的关键是运用S△AOB=S△AOC+S△BOC求解.求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解即可.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.下列式子一定是二次根式的是( )
| A. | $\sqrt{-x-2}$ | B. | $\sqrt{x}$ | C. | $\sqrt{{x}^{2}+2}$ | D. | $\sqrt{-5}$ |
6.下列方程中,是一元二次方程的是( )
| A. | 2x+1=0 | B. | y2+x=0 | C. | x2-x=0 | D. | $\frac{1}{x}$+x2=0 |
7. 如图,四边形ABCD的对角线AC、BD相交于点O,△ABO≌△ADO,下列结论
如图,四边形ABCD的对角线AC、BD相交于点O,△ABO≌△ADO,下列结论
①AC⊥BD;②CB=CD;③△ABC≌△ADC;④DA=DC,其中正确结论的序号是( )
 如图,四边形ABCD的对角线AC、BD相交于点O,△ABO≌△ADO,下列结论
如图,四边形ABCD的对角线AC、BD相交于点O,△ABO≌△ADO,下列结论①AC⊥BD;②CB=CD;③△ABC≌△ADC;④DA=DC,其中正确结论的序号是( )
| A. | ①② | B. | ②③④ | C. | ①②③ | D. | ①②④ |
4.2017年2月,微信公布《2017微信春节数据报告》,报告显示,除夕至初五,全国微信红包收发总量达到460亿个,同比去年增长43.3%,460亿用科学记数法可表示为( )
| A. | 4.60×102 | B. | 460×108 | C. | 4.60×109 | D. | 4.60×1010 |
 如图,长方形ABCD中,BE:EC=2:3,DF:FC=1:2,三角形DFG的面积为2平方厘米,求长方形的面积.
如图,长方形ABCD中,BE:EC=2:3,DF:FC=1:2,三角形DFG的面积为2平方厘米,求长方形的面积.