题目内容
7. 如图,四边形ABCD的对角线AC、BD相交于点O,△ABO≌△ADO,下列结论
如图,四边形ABCD的对角线AC、BD相交于点O,△ABO≌△ADO,下列结论①AC⊥BD;②CB=CD;③△ABC≌△ADC;④DA=DC,其中正确结论的序号是( )
| A. | ①② | B. | ②③④ | C. | ①②③ | D. | ①②④ |
分析 由全等三角形的性质可得∠AOB=∠AOD=90°,可判断①;由条件可得出AC垂直平分BD,可判断②;利用SSS可证明△ABC≌△ADC,可判断③;若DA=DC,则四边形ABCD为菱形,由条件无法判断,则可判断④,从而得出答案.
解答 解:
∵△ABO≌△ADO,
∴∠AOB=∠AOD,且∠AOB+∠AOD=180°,
∴∠AOB=∠AOD=90°,
∴AC⊥BD,故①正确;
∵BO=OD,
∴AC垂直平分BD,
∴BC=DC,故②正确;
在△ABC和△ADC中
$\left\{\begin{array}{l}{AB=AD}\\{BC=DC}\\{AC=AC}\end{array}\right.$
∴△ABC≌△ADC(SSS),故③正确;
若AD=DC,则可知AB=AD=DC=BC,
∴四边形ABCD为菱形时才有AD=DC成立,故④不正确;
综上可知正确的结论为①②③,
故选C.
点评 本题主要考查全等三角形的判定和性质,掌握全等三角形的对应边相等、对应角相等是解题的关键.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
17.计算:$\frac{{x}^{2}-x}{x}÷\frac{1-x}{2x}$=( )
| A. | -2x | B. | 2x | C. | -x | D. | x |
18.一组数据12,16,5,22,4,则这组数据的中位数是( )
| A. | 5 | B. | 12 | C. | 16 | D. | 22 |
2.随着移动互联网的不断普及,线上支付已经成为人们的生活方式和习惯,数据显示:截止2016年1月支付宝实名用户数量已经高达4.5亿,将这个数用科学记数法表示为( )
| A. | 4.5×107 | B. | 4.5×108 | C. | 4.5×109 | D. | 4.5×1010 |
12.2015年“双11”购物节,天猫平台交易额达到9 120 000万元,把9 120 000用科学记数法表示为( )
| A. | 912×108 | B. | 9.12×106 | C. | 9.12×108 | D. | 0.912×107 |
19. 一副三角板如图所示放置,则∠AOB等于( )
一副三角板如图所示放置,则∠AOB等于( )
 一副三角板如图所示放置,则∠AOB等于( )
一副三角板如图所示放置,则∠AOB等于( )| A. | 120° | B. | 90° | C. | 105° | D. | 60° |
16.-$\sqrt{3}$的绝对值是( )
| A. | -$\frac{1}{\sqrt{3}}$ | B. | -$\sqrt{3}$ | C. | $\sqrt{3}$ | D. | 5 |
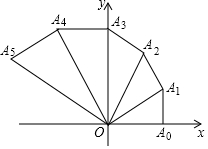 如图,Rt△OA0A1在平面直角坐标系内,∠OA0A1=90°,∠A0OA1=30°,以OA1为直角边向外作Rt△OA1A2,使∠OA1A2=90°,∠A1OA2=30°,以OA2为直角边向外作Rt△OA2A3,使∠OA2A3=90°,∠A2OA3=30°,按此方法进行下去,得到Rt△OA3A4,Rt△OA4A5,…,Rt△OA2016A2017,若点A0(1,0),则点A2017的横坐标为($\frac{\sqrt{3}}{2}$)2016.
如图,Rt△OA0A1在平面直角坐标系内,∠OA0A1=90°,∠A0OA1=30°,以OA1为直角边向外作Rt△OA1A2,使∠OA1A2=90°,∠A1OA2=30°,以OA2为直角边向外作Rt△OA2A3,使∠OA2A3=90°,∠A2OA3=30°,按此方法进行下去,得到Rt△OA3A4,Rt△OA4A5,…,Rt△OA2016A2017,若点A0(1,0),则点A2017的横坐标为($\frac{\sqrt{3}}{2}$)2016.