题目内容
已知P是直角三角形第二象限角平分线上的点,P到原点的距离是
,则点P的坐标是( )
| 2 |
| A、(1,1) |
| B、(-1,1) |
| C、(-1,-1) |
| D、(1,-1) |
考点:点的坐标
专题:数形结合
分析:根据第二象限角平分线上的点的坐标特征,设P(t,-t)(t<0),根据两点间的距离公式得到t2+(-t)2=(
)2,然后解方程求出t即可得到P点坐标.
| 2 |
解答:解:∵P是直角坐标系第二象限角平分线上的点,
∴点P的横纵坐标的绝对值相等,
设P(t,-t)(t<0),
∵P到原点的距离是
,
∴t2+(-t)2=(
)2,解得t1=-1,t2=1(舍去),
∴P点坐标为(-1,1).
故选B.
∴点P的横纵坐标的绝对值相等,
设P(t,-t)(t<0),
∵P到原点的距离是
| 2 |
∴t2+(-t)2=(
| 2 |
∴P点坐标为(-1,1).
故选B.
点评:本题考查了点的坐标:坐标平面内的点与有序实数对是一一对应的关系;记住各象限和坐标轴上点的坐标特征.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
某校为了了解七年级800名学生期中数学考试情况,从中抽取了100名学生的数学成绩进行了统计.下面5个判断中正确的有( )
①这种调查方式是抽样调查;②800名学生是总体;③每名学生的数学成绩是个体;④100名学生是总体的一个样本;⑤100名学生是样本容量.
①这种调查方式是抽样调查;②800名学生是总体;③每名学生的数学成绩是个体;④100名学生是总体的一个样本;⑤100名学生是样本容量.
| A、①② | B、①②④ |
| C、①③ | D、①③④⑤ |
下列调查方式中,应采用“普查”方式的是( )
| A、调查某品牌手机的市场占有率 |
| B、调查我市市民实施低碳生活的情况 |
| C、对我国首架歼15战机各个零部件的调查 |
| D、调查某型号炮弹的射程 |
已知点P在⊙O的内部,⊙O的半径为10cm,那么点P到⊙O的距离可以是( )
| A、9cm | B、10cm |
| C、11cm | D、12cm |
 如图,等边△ABC的边长为6,E是AC边上一点,AD是BC边上的中线,P是AD上的动点.若AE=2,则EP+CP的最小值为( )
如图,等边△ABC的边长为6,E是AC边上一点,AD是BC边上的中线,P是AD上的动点.若AE=2,则EP+CP的最小值为( )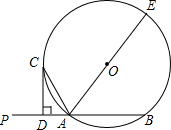 如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.
如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D. 如图是一个长为4cm,宽为3cm,高为5cm的长方体纸箱,则AC=
如图是一个长为4cm,宽为3cm,高为5cm的长方体纸箱,则AC=