题目内容
5．
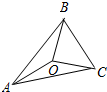如图，已知O是三角形ABC内一点，OA=OB=OC，∠ABC=70°，则∠AOC的大小为（ ）| A． | 70° | B． | 110° | C． | 140° | D． | 150° |
分析 根据等腰三角形的两个底角相等可得∠ABC+∠BAO+∠BCO的度数，根据三角形内角和定理可求∠CAO+∠ACO的度数，再根据三角形内角和定理可求∠AOC的度数．
解答 解：∵OA=OB=OC，
∴∠ABO=∠BAO，∠CBO=∠BCO，
∵∠ABC=70°，
∴∠ABC+∠BAO+∠BCO=140°，
∴∠CAO+∠ACO=40°，
∴∠AOC=140°．
故选C．
点评 本题考查了等腰三角形的两个底角相等的性质，三角形内角和等于180°的性质，求出∠CAO+∠ACO的度数是解题的关键．
练习册系列答案
相关题目