题目内容
17.下列四个选项中,变形正确的是( )| A. | a+(b+c)=ab+c | B. | a2-[-(-a+b)]-a2-a+b=a2-a+b | ||
| C. | a+2(b-c)=a+2b-c | D. | a-(b+c-d)=a-b-c+d |
分析 根据去括号的法则,可得答案.
解答 解:A、a+(b+c)=a+b+c,故A错误;
B、a2-[-(-a+b)]-a2-a+b=a2-[a-b]-a2-a+b=a2-a+b-a2-a+b=-2a+2b,故B错误;
C、a+2(b-c)=a+2b-2c,故C错误;
D、a-(b+c-d)=a-b-c+d,故D正确;
故选:D.
点评 本题考查了去括号,括号前是正数去括号不变号,括号前是负数去括号全变号.

练习册系列答案
相关题目
8.若函数y=(2m+1)x2+(1-2m)x+1(m为常数)是一次函数,则m的值为( )
| A. | m$>\frac{1}{2}$ | B. | m=$\frac{1}{2}$ | C. | m$<\frac{1}{2}$ | D. | m=-$\frac{1}{2}$ |
7.下列式子中结果为负数的是( )
| A. | |-2| | B. | -(-2) | C. | -|-2| | D. | (-2)2 |
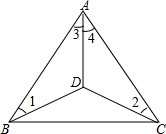 已知,如图△ABC中,BD=DC,∠1=∠2,求证:∠3=∠4.
已知,如图△ABC中,BD=DC,∠1=∠2,求证:∠3=∠4. 已知数a、b、c在数轴上的位置如图所示,化简|a+b|-|a-b|+|a+c|=a-c.
已知数a、b、c在数轴上的位置如图所示,化简|a+b|-|a-b|+|a+c|=a-c.