题目内容
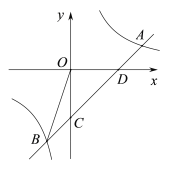
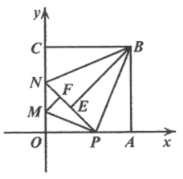
【题目】如图，在平面直角坐标系
第一象限中有正方形
，
，点
是
轴上一动点
，将
沿直线
翻折后，点
落在点
处。在
上有一点
，使得将
沿直线
翻折后，点
落在直线
上的点
处，直线交于点
，连接
.
I.求证：
；
Ⅱ.求
与
的函数关系式，并求出的最大值；
Ⅲ.当
时，直接写出的值.
【答案】I.见解析；Ⅱ.
，
，当
时，
的最大值为1；Ⅲ.
.
【解析】
I.根据邻补角的定义和角平分线的定义可得出
，从而证出
；
Ⅱ.结合I中结论和直角三角形的两锐角互余得出
，从而得出
，得到比例式得到t和m之间的函数关系式，根据配方法求出
的最大值.
Ⅲ. 先根据HL得出
，证出
，在AB上取一点Q，使得BQ=PQ，根据
，列出方程即可解决问题．
解：I.证明：∵
，
，
，
∴
.
∴，即.
Ⅱ.∵
，
，
∴.
∵四边形
是正方形，
，
，
∴
，
，
.
∴.
∴
.
∴
，
.
∴当
时，的最大值为1.
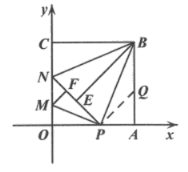
Ⅲ.如图，∵
，∴BC=AB,
∵
，∴BE=AB,
∴BC=BE,又∵BN=BN
∴
，
∴.
在
上取一点
使得
，
∴
.
∴
.
∴
.
∴
，
，
∵
，
∴
.
练习册系列答案
相关题目
