题目内容
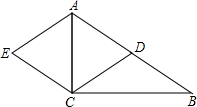 如图,在Rt△ABC中,∠ACB=90°,点D是斜边AB的中点,点A、C分别作AE∥CD,CE∥AB,CE、AE交于点E,求证:四边形ADCE是菱形.
如图,在Rt△ABC中,∠ACB=90°,点D是斜边AB的中点,点A、C分别作AE∥CD,CE∥AB,CE、AE交于点E,求证:四边形ADCE是菱形.考点:菱形的判定
专题:证明题
分析:首先根据平行四边形的定义证明四边形ADCE是平行四边形,然后根据直角三角形斜边上的中线等于斜边的一半,证明CD=AD,根据菱形的定义证明.
解答:证明:∵AE∥CD,CE∥AB,
∴四边形ADCE是平行四边形.
∵Rt△ABC中,∠ACB=90°,点D是斜边AB的中点,
∴CD=
AB=AD,
∴平行四边形ADCE是菱形.
∴四边形ADCE是平行四边形.
∵Rt△ABC中,∠ACB=90°,点D是斜边AB的中点,
∴CD=
| 1 |
| 2 |
∴平行四边形ADCE是菱形.
点评:本题考查了直角三角新的性质以及菱形的判定方法,理解菱形的判方法是关键.

练习册系列答案
相关题目
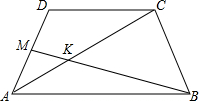 已知,如图,在梯形ABCD中,AB∥CD,M是AD中点,BM交AC于点K,AC=24cm,DC:AB=2:5,求AK、KC的长.
已知,如图,在梯形ABCD中,AB∥CD,M是AD中点,BM交AC于点K,AC=24cm,DC:AB=2:5,求AK、KC的长. 如图,AB、CD的两条互相垂直的直径,点O1、O2、O3、O4分别是OA、OB、OC、OD的中点.若⊙O的半径是2,求阴影部分的面积.
如图,AB、CD的两条互相垂直的直径,点O1、O2、O3、O4分别是OA、OB、OC、OD的中点.若⊙O的半径是2,求阴影部分的面积.