题目内容
18.已知|(a-b)2+1|+(a+b-2)2=1,x+ay=1,bx-y=3,则|(x-y)2+1|+(x+y-2)2=11.分析 利用非负数的性质求出a与b的值,代入已知方程求出x与y的值,即可确定出原式的值.
解答 解:∵|(a-b)2+1|+(a+b-2)2=1,
∴$\left\{\begin{array}{l}{a-b=0}\\{a+b=2}\end{array}\right.$,
解得:a=1,b=1,
代入得:$\left\{\begin{array}{l}{x+y=1}\\{x-y=3}\end{array}\right.$,
解得:x=2,y=-1,
则原式=10+1=11,
故答案为:11
点评 此题考查了解二元一次方程组,以及非负数的性质,熟练掌握运算法则是解本题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
 如图,∠AOB=96°,∠BOC=30°,OD、OE分别是∠AOB和∠BOC的角平分线,求:∠DOC的度数.
如图,∠AOB=96°,∠BOC=30°,OD、OE分别是∠AOB和∠BOC的角平分线,求:∠DOC的度数.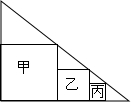 如图,一直角三角形中有三个连续排列的正方形甲、乙、丙,已知正方形甲、乙的边长分别为9、6,求正方形丙的边长.
如图,一直角三角形中有三个连续排列的正方形甲、乙、丙,已知正方形甲、乙的边长分别为9、6,求正方形丙的边长.