题目内容
14.若等腰三角形的顶角为120°,腰长为2cm,则它的底边长为2$\sqrt{3}$cm.分析 作AD⊥BC于点D,可得BC=2BD,RT△ABD中,根据BD=ABcos∠B求得BD,即可得答案.
解答 解:如图,作AD⊥BC于点D,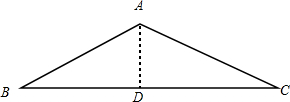
∵∠BAC=120°,AB=AC,
∴∠B=30°,
又∵AD⊥BC,
∴BC=2BD,
∵AB=2cm,
∴在RT△ABD中,BD=ABcos∠B=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$(cm),
∴BC=2$\sqrt{3}$cm,
故答案为:2$\sqrt{3}$.
点评 本题主要考查等腰三角形的性质及解直角三角形,熟练掌握等腰三角形的性质:①等腰三角形的两腰相等,②等腰三角形的两个底角相等. ③等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合是解题关键.

练习册系列答案
相关题目
5.太阳的半径为696000千米,把696000这个数据用科学记数法表示为( )
| A. | 696×103 | B. | 69.6×104 | C. | 6.96×105 | D. | 6.96×106 |
9.下列事件中的不可能事件是( )
| A. | 通常加热到100℃时,水沸腾 | |
| B. | 抛掷2枚正方体骰子,都是6点朝上 | |
| C. | 经过有交通信号灯的路口,遇到红灯 | |
| D. | 任意画一个三角形,其内角和是360° |
 如图,在平面直角坐标系中,Rt△ABC的顶点A,C分别在y轴,x轴上,∠ACB=90°,OA=$\frac{\sqrt{3}}{3}$,抛物线y=ax2-ax-a经过点B(2,$\sqrt{3}$),与y轴交于点D.
如图,在平面直角坐标系中,Rt△ABC的顶点A,C分别在y轴,x轴上,∠ACB=90°,OA=$\frac{\sqrt{3}}{3}$,抛物线y=ax2-ax-a经过点B(2,$\sqrt{3}$),与y轴交于点D.