题目内容
7.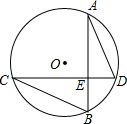 如图,⊙O中,弦AB⊥CD于E,若已知AD=6,BC=8,则⊙O的半径为5.
如图,⊙O中,弦AB⊥CD于E,若已知AD=6,BC=8,则⊙O的半径为5.
分析 连接DO并延长DO交圆O于点F,连接BD,AF,BF,根据圆周角登录得到∠DAE=∠DFB,∠AED=∠FBD=90°,根据三角形的内和得到∠ADC=∠FDB,由角的和差得到∠ADF=∠CDB,得到$\widehat{AF}=\widehat{BC}$,求得AF=BC=8,然后由勾股定理即可得到结论.
解答 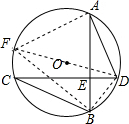 解:连接DO并延长DO交圆O于点F,连接BD,AF,BF,
解:连接DO并延长DO交圆O于点F,连接BD,AF,BF,
∵∠DAE=∠DFB,∠AED=∠FBD=90°,
∴∠ADC=∠FDB,
∴∠ADF=∠CDB,
∴$\widehat{AF}=\widehat{BC}$,
∴AF=BC=8,
∵∠DAF=90°,
∴DF=$\sqrt{A{F}^{2}+A{D}^{2}}$=$\sqrt{{8}^{2}+{6}^{2}}$=10,
∴⊙O的半径为5.
故答案为:5.
点评 本题考查了垂径定理,勾股定理,圆周角定理,正确的作出辅助线是解题的关键,

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
19.下列各式的合并不正确的是( )
| A. | 由3x-2x=1,得x=1 | B. | 由2x-3x=8,得-x=8 | ||
| C. | 由5x-2x+3x=12,得x=12 | D. | 由-7y+y=6,得-6y=6 |
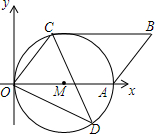 如图,在平面直角坐标系xOy中,点A在x轴正半轴上,OA=8,以OA为直径作⊙M,点C在⊙M上,∠AOC=45°,四边形ABCO为平行四边形.
如图,在平面直角坐标系xOy中,点A在x轴正半轴上,OA=8,以OA为直径作⊙M,点C在⊙M上,∠AOC=45°,四边形ABCO为平行四边形.
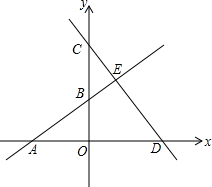 如图,直线AB:y=kx+b交x轴于点A(-3,0),交y轴于点B(0,2),交直线CD于点E,且E点的横坐标为3,直线CD交x轴于点D(10,0).
如图,直线AB:y=kx+b交x轴于点A(-3,0),交y轴于点B(0,2),交直线CD于点E,且E点的横坐标为3,直线CD交x轴于点D(10,0).