题目内容
17.若a2-6a+9与|b-2|互为相反数,则式子($\frac{a}{b}$-$\frac{b}{a}$)÷(a+b)的值为$\frac{1}{6}$.分析 根据相反数及非负数的性质“两个非负数相加,和为0,这两个非负数的值都为0”求出a、b的值,再代入所求代数式计算即可.
解答 解:由题意知a2-6a+9+|b-2|=(a-3)2+|b-2|=0,
∴a-3=0,b-2=0,
∴a=3,b=2.
($\frac{a}{b}$-$\frac{b}{a}$)÷(a+b)=$\frac{\frac{a}{b}-\frac{b}{a}}{a+b}=\frac{\frac{{a}^{2}-{b}^{2}}{ab}}{a+b}=\frac{a-b}{ab}=\frac{3-2}{3×2}=\frac{1}{6}$,
故答案为:$\frac{1}{6}$
点评 本题考查了非负数的性质.
初中阶段有三种类型的非负数:
(1)绝对值;
(2)偶次方;
(3)二次根式(算术平方根).
当它们相加和为0时,必须满足其中的每一项都等于0.根据这个结论可以求解这类题目.

练习册系列答案
相关题目
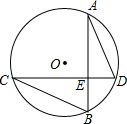 如图,⊙O中,弦AB⊥CD于E,若已知AD=6,BC=8,则⊙O的半径为5.
如图,⊙O中,弦AB⊥CD于E,若已知AD=6,BC=8,则⊙O的半径为5.