题目内容
18.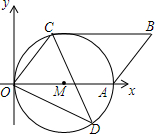 如图,在平面直角坐标系xOy中,点A在x轴正半轴上,OA=8,以OA为直径作⊙M,点C在⊙M上,∠AOC=45°,四边形ABCO为平行四边形.
如图,在平面直角坐标系xOy中,点A在x轴正半轴上,OA=8,以OA为直径作⊙M,点C在⊙M上,∠AOC=45°,四边形ABCO为平行四边形.(1)求证:BC为⊙M的切线.
(2)求点B的坐标.
(3)若D点坐标为(3$\sqrt{3}$,-3),求∠OCD的正弦值.
分析 (1)连接CM,求出∠OCM=∠COA=45°,求出∠CMA=90°,根据平行四边形的性质求出∠BCM=∠CMA即可;
(2)求出OM和CM值,即可求出B的坐标;
(3)连接AD,过D作DN⊥OA于N,根据D的坐标求出DO的值,得出∠OAD=∠OCD,在Rt△AND中,根据解直角三角形求出即可.
解答 (1)证明: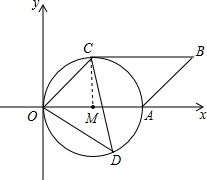 连接CM,
连接CM,
∵OM=CM,∠AOC=45°,
∴∠AOC=∠OCM=45°,
∴∠CMA=45°+45°=90°,
∵四边形ABCO是平行四边形,
∴BC∥OA,
∴∠BCM=180°-90°=90°,
∴MC⊥BC,
∵MC是半径,
∴BC是⊙M的切线;
(2)解:∵OA=8,
∴OM=4,
∴MC=OM=4,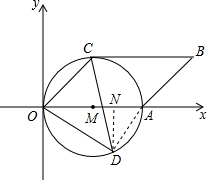
∴B的横坐标是4+8=12,
即B的坐标是(12,4);
(3)解:连接AD,过D作DN⊥OA于N,
∵D(3$\sqrt{3}$,-3),
∴ON=3$\sqrt{3}$,DN=3,
∴DO=$\sqrt{{ON}^{2}{+DN}^{2}}$=$\sqrt{{(3\sqrt{3})}^{2}{+3}^{2}}$=6,
∵OA=8,
由圆周角定理得:∠OAD=∠OCD,
即sin∠OCD=sin∠OAD=$\frac{OD}{OA}$=$\frac{3}{4}$.
点评 本题主要考查了平行四边形性质,解直角三角形,切线的判定,圆周角定理等知识点的应用,作出适当的辅助线是解答此题的关键.

练习册系列答案
相关题目
8.若方程x-(2a+1)=3x+(3a+2)的解是x=0,则a等于( )
| A. | $\frac{1}{5}$ | B. | $\frac{3}{5}$ | C. | -$\frac{1}{5}$ | D. | -$\frac{3}{5}$ |
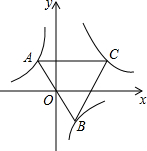 如图,已知点A是双曲线y=-$\frac{2}{x}$在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第一象限内,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$(k>0)上运动,则k的值是6.
如图,已知点A是双曲线y=-$\frac{2}{x}$在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第一象限内,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$(k>0)上运动,则k的值是6.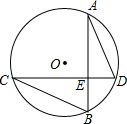 如图,⊙O中,弦AB⊥CD于E,若已知AD=6,BC=8,则⊙O的半径为5.
如图,⊙O中,弦AB⊥CD于E,若已知AD=6,BC=8,则⊙O的半径为5.