Question

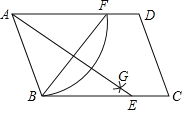
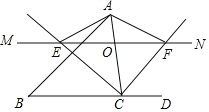
【题目】如图，在矩形中，连接点为上一点，使得连接交于点，作交的延长线于点．

（1）求证：．

（2）若求的长．

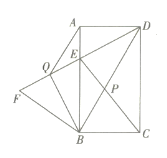
（3）在（2）的条件下，将沿着对折得到点的对应点为点，连接试求的周长．

Answer 1

【答案】（1）详见解析；（2）；（3）的周长

【解析】

（1）由矩形的性质得∠BCD=∠FBD，结合∠BCD=∠FBD，可得，进而即可得到结论；

（2）先证，再证BE=DE=EF，结合，求出BD的长，从而的BC，EC的长，由，得，即可求解；

（3）由折叠的性质得QE=1，从而得AE=QE，再证，进而即可求解．

（1）∵在矩形中，

∴∠BCD=90°，

∵，

∴∠BCD=∠FBD，

又∵，

，

，

；

（2），

，

又∵，

，

．

又，

．

，

，

由（1）可知：，

，

，

，

，

，

，即，

解得：；

（3）沿对折得到，，

点在上，且，

∴DQ=DC=3，

∵DE=BE=2，

，

，

．

∵BE=DE，

∴∠EBD=∠EDB，

又，

∴=∠EBD=∠EDB，

，

的周长：的周长，

的周长，

的周长．