题目内容
17.若二次函数y=x2+mx的对称轴是x=2,则关于x的方程x2+mx=5的解为( )| A. | x1=0,x2=5 | B. | x1=1,x2=5 | C. | x1=1,x2=-5 | D. | x1=-1,x2=5 |
分析 先根据二次函数y=x2+mx的对称轴是x=2求出m的值,再把m的值代入方程x2+mx=5,求出x的值即可.
解答 解:∵二次函数y=x2+mx的对称轴是x=2,
∴-$\frac{m}{2}$=2,解得m=-4,
∴关于x的方程x2+mx=5可化为x2-4x-5=0,即(x+1)(x-5)=0,解得x1=-1,x2=5.
故选D.
点评 本题考查的是二次函数的性质,熟知二次函数的对称轴方程是解答此题的关键.

练习册系列答案
相关题目
7.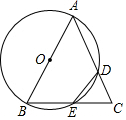 如图,在△ABC中,AB=AC,以AB为直径的圆分别交边AC,BC于点D,E,若$\widehat{AD}$=$\widehat{DE}$+30°,则∠DEC的度数是( )
如图,在△ABC中,AB=AC,以AB为直径的圆分别交边AC,BC于点D,E,若$\widehat{AD}$=$\widehat{DE}$+30°,则∠DEC的度数是( )
 如图,在△ABC中,AB=AC,以AB为直径的圆分别交边AC,BC于点D,E,若$\widehat{AD}$=$\widehat{DE}$+30°,则∠DEC的度数是( )
如图,在△ABC中,AB=AC,以AB为直径的圆分别交边AC,BC于点D,E,若$\widehat{AD}$=$\widehat{DE}$+30°,则∠DEC的度数是( )| A. | 30° | B. | 40° | C. | 45° | D. | 50° |
5.已知点M(a,2),点N(3,b)关于y轴对称,则(a+b)2016=( )
| A. | -3 | B. | -1 | C. | 1 | D. | 3 |
9.在下列代数式中,次数为3的单项式是( )
| A. | x2y | B. | xy3 | C. | x3+y3 | D. | 3xy |
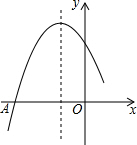 如图,二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1.
如图,二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1.