题目内容
1.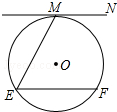 如图,直线MN与⊙O相切于点M,ME=EF且EF∥MN,则∠E的大小等于( )
如图,直线MN与⊙O相切于点M,ME=EF且EF∥MN,则∠E的大小等于( )| A. | 75° | B. | 60° | C. | 45° | D. | 30° |
分析 连接OM,OM的反向延长线交EF于点C,由直线MN与⊙O相切于点M,根据切线的性质得OM⊥MN,而EF∥MN,根据平行线的性质得到MC⊥EF,于是根据垂径定理有CE=CF,再利用等腰三角形的判定得到ME=MF,易证得△MEF为等边三角形,所以∠E=60°.
解答 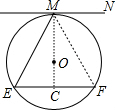 解:连接OM,OM的反向延长线交EF于点C,如图,
解:连接OM,OM的反向延长线交EF于点C,如图,
∵直线MN与⊙O相切于点M,
∴OM⊥MN,
∵EF∥MN,
∴MC⊥EF,
∴CE=CF,
∴ME=MF,
而ME=EF,
∴ME=EF=MF,
∴△MEF为等边三角形,
∴∠E=60°,
故选B.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了垂径定理、等边三角形的判定与性质和特殊角的三角函数值.

练习册系列答案
相关题目
12.已知在等腰△ABC中,顶角∠A=36°,BD平分∠ABC交AC于点D,则下列说法中错误的是( )
| A. | △ABC∽△BDC | B. | 点D是线段AC的黄金分割点 | ||
| C. | $\frac{AD}{AC}$=$\frac{\sqrt{5}-1}{2}$ | D. | $\frac{AD}{AC}$=$\frac{1}{2}$ |
16.下列图形都是由同样大小的五角星按一定的规律组成,其中第①个图形有1个五角星,第②个图形有5个五角星,第③个图形有13个五角星…,则第⑥个图形中五角星的个数为( )


| A. | 41 | B. | 53 | C. | 57 | D. | 61 |
6.下列条件中,可以确定△ABC和△A′B′C′全等的是( )
| A. | BC=BA,B′C′=B′A′,∠B=∠B′ | B. | ∠A=∠B′,AC=A′B′,AB=B′C′ | ||
| C. | ∠A=∠A′,AB=B′C′,AC=A′C′ | D. | BC=B′C′,AC=A′B′,∠B=∠C′ |
13.关于x的一元二次方程(a-1)x2+x+a2-1=0的一个根0,则a值为( )
| A. | 1 | B. | -1 | C. | ±1 | D. | 0 |
10. 如图,数轴上有A,B,C,D四个点,其中表示-3的相反数的点是( )
如图,数轴上有A,B,C,D四个点,其中表示-3的相反数的点是( )
 如图,数轴上有A,B,C,D四个点,其中表示-3的相反数的点是( )
如图,数轴上有A,B,C,D四个点,其中表示-3的相反数的点是( )| A. | 点A | B. | 点B | C. | 点C | D. | 点D |
11.在学习“用直尺和圆规作一个角等于已知角”时,教科书介绍如图:对于“想一想”中的问题,下列回答正确的是( )


| A. | 根据“边边边”可知,△C′O′D′≌△COD,所以∠A′O′B′=∠AOB | |
| B. | 根据“边角边”可知,△C′O′D′≌△COD,所以∠A′O′B′=∠AOB | |
| C. | 根据“角边角”可知,△C′O′D′≌△COD,所以∠A′O′B′=∠AOB | |
| D. | 根据“角角边”可知,△C′O′D′≌△COD,所以∠A′O′B′=∠AOB |