题目内容
已知关于x的一元二次方程x2+2(m-1)x+m2-1=0.
(1)若方程有两个不相等的实数根,求实数m的取值范围;
(2)若方程的一个根为0,求出m的值及方程的另一个根.
(1)若方程有两个不相等的实数根,求实数m的取值范围;
(2)若方程的一个根为0,求出m的值及方程的另一个根.
考点:根的判别式,根与系数的关系
专题:计算题
分析:(1)根据判别式的意义得到△=4(m-1)2-4(m2-1)>0,然后解不等式即可;
(2)根据方程解的定义把x=0代入方程得m2-1=0,即可解得m=1或-1,然后分别把m=1或m=-1代入方程,再解方程即可.
(2)根据方程解的定义把x=0代入方程得m2-1=0,即可解得m=1或-1,然后分别把m=1或m=-1代入方程,再解方程即可.
解答:解:(1)根据题意得△=4(m-1)2-4(m2-1)>0,
解得m<1;
(2)把x=0代入方程得m2-1=0,解得m=1或-1,
当m=1时,方程变形为x2=0,解得x1=x2=0,即方程的另一个根为0;
当m=-1时,方程变形为x2-4x=0,解得x1=4,x2=0,即方程的另一个根为4.
解得m<1;
(2)把x=0代入方程得m2-1=0,解得m=1或-1,
当m=1时,方程变形为x2=0,解得x1=x2=0,即方程的另一个根为0;
当m=-1时,方程变形为x2-4x=0,解得x1=4,x2=0,即方程的另一个根为4.
点评:本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
下列说法中不正确的是( )
| A、函数y=2(x-1)2-1的一次项系数是-4 |
| B、“明天降雨的概率是50%”表示明天有半天都在降雨 |
| C、若a为实数,则|a|<0是不可能事件 |
| D、一个盒子中有白球m个,红球6个,黑球n个(每个球除了颜色外都相同),如果从中任取一个球,取得的是红球的概率与不是红球的概率相同,那么m与n的和是6 |
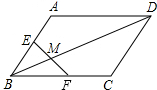 已知,如图在?ABCD中点E,F分别是AB,BC的中点,BD与EF相交于点M,求证:EM=FM.
已知,如图在?ABCD中点E,F分别是AB,BC的中点,BD与EF相交于点M,求证:EM=FM.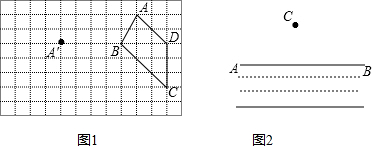
 甲、乙两人用如图的两个分格均匀的转盘A、B做游戏,游戏规则如下:分别转动两个转盘,转盘停止后,指针分别指向一个数字(若指针停止在等份线上,那么重转一次,直到指针指向某一数字为止),用所指的两个数字相乘,如果积是奇数,则甲获胜;如果积是偶数,则乙获胜,请你解决下列问题:
甲、乙两人用如图的两个分格均匀的转盘A、B做游戏,游戏规则如下:分别转动两个转盘,转盘停止后,指针分别指向一个数字(若指针停止在等份线上,那么重转一次,直到指针指向某一数字为止),用所指的两个数字相乘,如果积是奇数,则甲获胜;如果积是偶数,则乙获胜,请你解决下列问题:
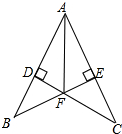 如图,BE⊥AC于点E,CD⊥AB于点D,BE、CD交于F,且AF平分∠BAC,求证:BF=FC.
如图,BE⊥AC于点E,CD⊥AB于点D,BE、CD交于F,且AF平分∠BAC,求证:BF=FC.