题目内容
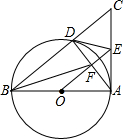 如图,Rt△ABC中,∠BAC=90°,以AB为直径作⊙O交BC于点D,OE∥BC交AC于点E,连接AD,交OE于点F,连接DE.
如图,Rt△ABC中,∠BAC=90°,以AB为直径作⊙O交BC于点D,OE∥BC交AC于点E,连接AD,交OE于点F,连接DE.(1)判断DE与⊙O的位置关系,并证明;
(2)连接BF,若⊙O的半径为4,AE=3,求BF的长.
考点:切线的判定,勾股定理,相似三角形的判定与性质
专题:
分析:(1)连接OD,由AB为⊙O的直径,得∠BDA=90°,由OE∥BC,可得∠OFA=∠BDA=90°,再由OA=OD得∠AOF=∠DOF,即可证明△ODE≌△OAE,得∠ODE=∠OAE=90°,得OD⊥DE,所以DE为⊙O的切线,即DE与⊙O相切
(2)因为OA=4,AE=3,所以由勾股定理得OE=5,由O点为AB的中点,OE∥BC,所以点E为AC的中点,可得OE为△BAC的中位线,由射影定理得,BD,AD,在Rt△BDF中,由勾股定理得BF即可.
(2)因为OA=4,AE=3,所以由勾股定理得OE=5,由O点为AB的中点,OE∥BC,所以点E为AC的中点,可得OE为△BAC的中位线,由射影定理得,BD,AD,在Rt△BDF中,由勾股定理得BF即可.
解答: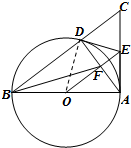 答:(1)DE与⊙O相切.
答:(1)DE与⊙O相切.
证明:连接OD,
∵AB为⊙O的直径,
∴∠BDA=90°,
∵OE∥BC,
∴∠OFA=∠BDA=90°,
∵OA=OD,
∴∠AOF=∠DOF,
又OE=OE,
∴△ODE≌△OAE(SAS),
∴∠ODE=∠OAE=90°,
∴OD⊥DE,
∴DE为⊙O的切线,即DE与⊙O相切,
(2)解:∵OA=4,AE=3,
∴由勾股定理得OE=5,
∵O点为AB的中点,OE∥BC,
∴点E为AC的中点,
∴OE为△BAC的中位线,
∴BA=2OA=8,AC=2AE=6,BC=2OE=10,
由射影定理得,BD=
,AD=
∴DF=
AD=
,
在Rt△BDF中,由勾股定理得:
BF=
=
=
,
则BF的长是
.
 答:(1)DE与⊙O相切.
答:(1)DE与⊙O相切.证明:连接OD,
∵AB为⊙O的直径,
∴∠BDA=90°,
∵OE∥BC,
∴∠OFA=∠BDA=90°,
∵OA=OD,
∴∠AOF=∠DOF,
又OE=OE,
∴△ODE≌△OAE(SAS),
∴∠ODE=∠OAE=90°,
∴OD⊥DE,
∴DE为⊙O的切线,即DE与⊙O相切,
(2)解:∵OA=4,AE=3,
∴由勾股定理得OE=5,
∵O点为AB的中点,OE∥BC,
∴点E为AC的中点,
∴OE为△BAC的中位线,
∴BA=2OA=8,AC=2AE=6,BC=2OE=10,
由射影定理得,BD=
| 32 |
| 5 |
| 24 |
| 5 |
∴DF=
| 1 |
| 2 |
| 12 |
| 5 |
在Rt△BDF中,由勾股定理得:
BF=
| BD2+DF2 |
(
|
4
| ||
| 5 |
则BF的长是
4
| ||
| 5 |
点评:本题考查了切线的判定、勾股定理以及相似三角形的判定和性质.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知
是二元一次方程组
的解,则
的算术平方根为( )
|
|
| m+3n |
| A、±3 | ||
| B、3 | ||
C、
| ||
D、±
|
 为了增强体质并迎接即将到来的体育中考,全校学生积极参加体育锻炼,学校教务处对学生锻炼时间做了一抽样调查,记录了部分学生锻炼时间如下:
为了增强体质并迎接即将到来的体育中考,全校学生积极参加体育锻炼,学校教务处对学生锻炼时间做了一抽样调查,记录了部分学生锻炼时间如下: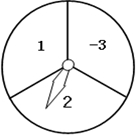 如图转盘,分成三个相同的扇形,3个扇形分别标有数字1、2、-3,指针位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置,并相应得到一个数(指针指向两个扇形的交线时,重新转动转盘).
如图转盘,分成三个相同的扇形,3个扇形分别标有数字1、2、-3,指针位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置,并相应得到一个数(指针指向两个扇形的交线时,重新转动转盘).