Question

9．如图，己知点P从边长为1的正方形ABCD的顶点B出发，沿着BC边向点C方向运动，到点P与C点重合时停止，连接AP并以AP为直角边在AP右侧作等腰直角△APQ，其中∠APQ=90°，则在运动过程中，点Q所经过的路程长为（　　）

• A． $\sqrt{2}$
• B． 2
• C． $\frac{\sqrt{2}}{2}$π
• D． $\frac{\sqrt{2}}{3}$π

Answer 1

分析 如图，延长AD到M，使得DM=AD，连接CM，则点Q运动轨迹是线段CM．只要证明△ABP≌△PNQ，CN=QN即可解决问题．

解答 解：如图，延长AD到M，使得DM=AD，连接CM，则点Q运动轨迹是线段CM．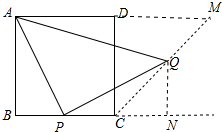

作QN⊥BC于N，
∵PA=PQ，∠APQ=90°，
∴∠APB+∠QPN=90°，∠QPN+∠PQN=90°，
∴∠APB=∠PQN，
在△ABP和△PNQ中，
$\left\{\begin{array}{l}{∠B=∠PNQ=90°}\\{∠APB=∠PQN}\\{AP=PQ}\end{array}\right.$，
∴△ABP≌△PNQ，
∴AB=PN=BC，PB=NQ，
∴PB=CN=QN，
∴∠QCN=45°，
∴点Q在线段CM上，点Q的运动轨迹是线段CM，
CM=$\sqrt{2}$CD=$\sqrt{2}$．
故选A．

点评 本题考查正方形的性质、等腰直角三角形的性质、全等三角形的判定和性质、轨迹等知识，解题的关键是学会添加常用辅助线，构造全等三角形，属于中考常考题型．