题目内容
15.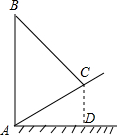 如图,是斜坡AC上一根电线杆AB用钢丝绳BC进行固定的平面图.已知斜坡AC的长度为8m,钢丝绳BC的长度为10m,AB⊥AD于点A,CD⊥AD于点D,若CD=4,则电线杆AB的高度是多少m?(结果保留根号)
如图,是斜坡AC上一根电线杆AB用钢丝绳BC进行固定的平面图.已知斜坡AC的长度为8m,钢丝绳BC的长度为10m,AB⊥AD于点A,CD⊥AD于点D,若CD=4,则电线杆AB的高度是多少m?(结果保留根号)
分析 过点C作CE∥AD交AB于点E,得到矩形ADCE,那么AE=CD=4,CE=AD.先在直角△ACD中利用勾股定理求出AD,然后在直角△BCE中利用勾股定理求出BE,那么AB=AE+BE.
解答 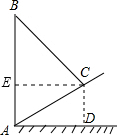 解:过点C作CE∥AD交AB于点E,
解:过点C作CE∥AD交AB于点E,
∵AB⊥AD于点A,CD⊥AD于点D,
∴四边形ADCE是矩形,
∴AE=CD=4,CE=AD.
在直角△ACD中,∵∠ADC=90°,
∴AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=$\sqrt{{8}^{2}-{4}^{2}}$=4$\sqrt{3}$,
∴CE=AD=4$\sqrt{3}$.
在直角△BCE中,∵∠BEC=90°,
∴BE=$\sqrt{B{C}^{2}-C{E}^{2}}$=$\sqrt{1{0}^{2}-(4\sqrt{3})^{2}}$=2$\sqrt{13}$,
∴AB=AE+BE=4+2$\sqrt{13}$.
即电线杆AB的高度是(4+2$\sqrt{13}$)m.
点评 本题考查了勾股定理的应用,准确作出辅助线求出BE的长是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.下列给出的点中,在函数y=-2x+1的图象上的点是( )
| A. | (1,3) | B. | (-2.5,-4) | C. | (2.5,-4) | D. | (-1,1) |
12. 一个不等式组的解集在数轴上的表示如图,则这个不等式组的解集是( )
一个不等式组的解集在数轴上的表示如图,则这个不等式组的解集是( )
 一个不等式组的解集在数轴上的表示如图,则这个不等式组的解集是( )
一个不等式组的解集在数轴上的表示如图,则这个不等式组的解集是( )| A. | -1<x<3 | B. | -1<x≤3 | C. | -1≤x<3 | D. | -1≤x≤3 |
 如图,一次函数y=kx+b(k<0)的图象过点(0,-2),则不等式kx+b<-2的解集是x>0.
如图,一次函数y=kx+b(k<0)的图象过点(0,-2),则不等式kx+b<-2的解集是x>0.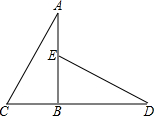 已知:如图,AB⊥CD,垂足为B,点E在AB上,AB=BD,BE=BC,求证:△ABC≌△DBE.
已知:如图,AB⊥CD,垂足为B,点E在AB上,AB=BD,BE=BC,求证:△ABC≌△DBE.