题目内容
6.已知y=-2x2-4x+7,根据下列x的范围求函数y的最值(1)-3≤x≤-2
(2)-3≤x≤0
(3)-3≤x≤3
(4)0≤x≤3.
分析 先求得二次函数的对称轴;
(1)根据对称轴在-3≤x≤-2内的情况,即可求得二次函数的最大值和最小值;
(2)根据对称轴在-3≤x≤0内的情况,即可求得二次函数的最大值,再根据二次函数关于对称轴对称,找到距离对称轴最远的点,即可求得当-3≤x≤0时,二次函数的最小值.
(3)根据对称轴在-3≤x≤3内的情况,即可求得二次函数的最大值,再根据二次函数关于对称轴对称,找到距离对称轴最远的点,即可求得当-3≤x≤3时,二次函数的最小值.
(4)根据对称轴在0≤x≤-2内的情况,即可求得二次函数的最大值和最小值.
解答 解:∵二次函数y=-2x2-4x+7对称轴为y=-$\frac{b}{2a}$=-1,且a=-2<0,
(1)当-3≤x≤-2时,x=-3时,二次函数y有最小值为y=-2×(-3)2-4×(-3)+7=1,x=-2时,二次函数y有最大值为y=-2×(-2)2-4×(-2)+7=7;
(2)当-3≤x≤0时,x=-1时,二次函数y有最大值为y=-2×(-1)2-4×(-1)+7=9,
∵|-3-(-1)|=2,|0-(-1)|=1,
∴x=-3时,二次函数y有最小值为y=-2×(-3)2-4×(-3)+7=1;
(3)当-3≤x≤3时,x=-1时,二次函数y有最大值为y=-2×(-1)2-4×(-1)+7=9,
∵|-3-(-1)|=2,|3-(-1)|=4,
∴x=3时,二次函数y有最小值为y=-2×32-4×3+7=-23;
(4)当0≤x≤3时,x=0时,二次函数y有最大值为y=7,x=3时,二次函数y有最小值为y=-2×32-4×3+7=-23.
点评 本题考查了二次函数对称轴的求解,考查了二次函数的最值问题,本题中求得二次函数的对称轴是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.已知a>0,则下列计算正确的是( )
| A. | $\sqrt{a}$+$\sqrt{a}$=$\sqrt{2a}$ | B. | $\sqrt{{a}^{2}}$-$\sqrt{a}$=$\sqrt{a}$ | C. | $\sqrt{a}×\sqrt{a}$=a2 | D. | $\sqrt{a}$$÷\sqrt{a}$=1 |
 如图,是小明学习三线八角时制作的模具,经测量∠2=100°,要使木条a与b平行,则∠1的度数必须是80°.
如图,是小明学习三线八角时制作的模具,经测量∠2=100°,要使木条a与b平行,则∠1的度数必须是80°. 如图,△ABC中,∠B,∠C的平分线交于P,∠A=90°,求∠P.
如图,△ABC中,∠B,∠C的平分线交于P,∠A=90°,求∠P.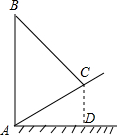 如图,是斜坡AC上一根电线杆AB用钢丝绳BC进行固定的平面图.已知斜坡AC的长度为8m,钢丝绳BC的长度为10m,AB⊥AD于点A,CD⊥AD于点D,若CD=4,则电线杆AB的高度是多少m?(结果保留根号)
如图,是斜坡AC上一根电线杆AB用钢丝绳BC进行固定的平面图.已知斜坡AC的长度为8m,钢丝绳BC的长度为10m,AB⊥AD于点A,CD⊥AD于点D,若CD=4,则电线杆AB的高度是多少m?(结果保留根号)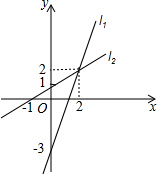 已知l1、l2的解析式分别为y1=ax+b,y2=mx+n(a>m>0),如图是l1、l2的图象,根据图象回答以下问题:
已知l1、l2的解析式分别为y1=ax+b,y2=mx+n(a>m>0),如图是l1、l2的图象,根据图象回答以下问题: