题目内容
已知弓形的半径为5cm，弦长为8cm，则弓形的高为 ．
考点：扇形面积的计算
专题：
分析：过O作直径OC⊥AB于D，连接OA，则CD是弓形的高或DE是弓形的高，根据垂径定理求出AD，根据勾股定理求出OD，即可求出答案．
解答：
解：过O作直径OC⊥AB于D，连接OA，则CD是弓形的高或DE是弓形的高，
∵CE⊥AB，CE为直径，
∴AD=DB=
AB=4cm，
在Rt△ADO中，由勾股定理得：AO2=AD2+OD2，
52=42+OD2，
OD=3，
∴CD=5cm-3cm=2cm，DE=5cm+3cm=8cm．
故答案为：2cm或8cm．
解：过O作直径OC⊥AB于D，连接OA，则CD是弓形的高或DE是弓形的高，∵CE⊥AB，CE为直径，
∴AD=DB=
| 1 |
| 2 |
在Rt△ADO中，由勾股定理得：AO2=AD2+OD2，
52=42+OD2，
OD=3，
∴CD=5cm-3cm=2cm，DE=5cm+3cm=8cm．
故答案为：2cm或8cm．
点评：本题考查了垂径定理和勾股定理的应用，根据题意画出图形，利用数形结合求解是解答此题的关键．
练习册系列答案
名校课堂系列答案
相关题目
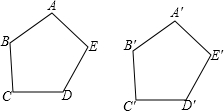如图，在五边形ABCDE和五边形A1B1C1D1E1中，如果AB=A1B1，BC=B1C1，CD=C1D1，DE=D1E1，EA=E1A1．请添加尽可能少的条件，使它们全等（写出添加的条件，不需要说明理由）
已知线段AB，请用尺规按下列要求作图（不写作法，只保留作图痕迹）：
