题目内容
一种新运算，规定有以下两种变换：
①f（m，n）=（m，-n）．如f（3，2）=（3，-2）；
②g（m，n）=（-m，-n），如g（3，2）=（-3，-2）．
按照以上变换有f[g（3，4）]=f（-3，-4）=（-3，4），那么g[f（5，-6）]等于 ．
①f（m，n）=（m，-n）．如f（3，2）=（3，-2）；
②g（m，n）=（-m，-n），如g（3，2）=（-3，-2）．
按照以上变换有f[g（3，4）]=f（-3，-4）=（-3，4），那么g[f（5，-6）]等于
考点：有理数的混合运算
专题：新定义
分析：根据题中的两种变换化简所求式子，计算即可得到结果．
解答：解：根据题意得：g[f（5，-6）]=g（5，6）=（-5，-6）．
故答案为：（-5，-6）．
故答案为：（-5，-6）．
点评：此题考查了有理数的混合运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
智趣暑假温故知新系列答案
相关题目
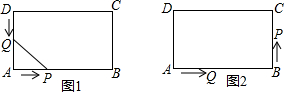如图1，在长方形ABCD中，AB=12厘米，BC=6厘米．点P沿AB边从点A开始向点B以2厘米/秒的速度移动；点Q沿DA边从点D开始向点A以1厘米/秒的速度移动．如果P、Q同时出发，用t（秒）表示移动的时间，那么：
如图，已知点E、C在线段BF上，BE=CF，请在下列四个等式中：①AB=DE，②∠ACB=∠F，③∠A=∠D，④AC=DF．选出两个作为条件，推出△ABC≌△DEF．并予以证明．（写出一种即可）
如图，直线y=-
将一副三角尺如图所示叠放在一起，则∠AEC的度数是
如图，已知△ABC≌△FED，∠A=40°，∠B=80°，则∠EDF=