题目内容
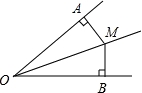
如图,已知∠AOB=40°,OM平分∠AOB,MA⊥OA,MB⊥OB,垂足分别为A、B两点,则∠MAB等于( )
A.50° B.40° C.30° D.20°
D【考点】角平分线的性质;三角形内角和定理.
【分析】由角平分线的性质可得MA=MB,再求解出∠MAB的大小,在△ABM中,则可求解∠MAB的值.
【解答】解:∵∠AOB=40°,且OM为其平分线,∴∠AOM=∠BOM=20°,
又MA⊥OA,MB⊥OB,∴MA=MB,∠AMO=∠BMO=70°,
∴∠AMB=140°,
∴∠MAB= (180°﹣∠AMB)=
(180°﹣∠AMB)= ×(180°﹣140°)=20°,故选D.
×(180°﹣140°)=20°,故选D.
【点评】本题考查了角平分线的性质;熟练掌握角平分 线的性质,能够求解一些简单的计算问题.
线的性质,能够求解一些简单的计算问题.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
 x>0)千米,在B市乘坐出租车y(y>0)千米.
x>0)千米,在B市乘坐出租车y(y>0)千米.

 .
.