题目内容
4.将正面分别标有数字1,2,3,4,6,背面花色相同的五张卡片洗匀后,背面朝上放在桌面上,从中随机抽取一张,不放回,再从中随机抽取一张.(1)求抽出的两张卡片上的数字恰好相邻的概率.
(2)抽得的第一张卡片上的数字记为a,第二张卡片上的数字记为b,求点P(a,b)在直线y=x-2上的概率.
分析 (1)先画树状图展示所有20种等可能的结果数,再找出抽出的两张卡片上的数字恰好相邻的结果数,然后根据概率公式求解;
(2)根据一次函数图象上点的坐标特征可判断点(3,1),(4,2),(6,4)在直线y=x-2上,然后根据概率公式求解.
解答 解:(1)画树状图为:
共有20种等可能的结果数,抽出的两张卡片上的数字恰好相邻的结果数为4,
所以抽出的两张卡片上的数字恰好相邻的概率=$\frac{4}{20}$=$\frac{1}{5}$;
(2)点(3,1),(4,2),(6,4)在直线y=x-2上,
即点P(a,b)在直线y=x-2上的结果数为3,
所以点P(a,b)在直线y=x-2上的慨率=$\frac{3}{20}$.
点评 本题考查了列表法与树状图法:利用列表法和树状图法展示所有可能的结果求出n,再从中选出符合事件A或B的结果数目m,求出概率.也考查了一次函数图象上点的坐标特征.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
19.若|x|=-x,那么x的取值范围是( )
| A. | x≥0 | B. | x≤0 | C. | x>0 | D. | x<0 |
 △ABC中,G是△ABC的重心,过G作EF∥AC,求S△BEF:S△ACG.
△ABC中,G是△ABC的重心,过G作EF∥AC,求S△BEF:S△ACG. 如图,玲玲用丝线和印有6行6列方格图的布给她的小猫绣了一个星星图案的饰物.小猫去抓这个饰物时.抓到丝线(阴影部分)的概率是多大?
如图,玲玲用丝线和印有6行6列方格图的布给她的小猫绣了一个星星图案的饰物.小猫去抓这个饰物时.抓到丝线(阴影部分)的概率是多大?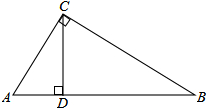 如图,Rt△ABC中,∠ACB=90°,CD⊥AB于D,AC=$\sqrt{3}$,BC=$\sqrt{6}$,求∠BCD的三个角函数值.
如图,Rt△ABC中,∠ACB=90°,CD⊥AB于D,AC=$\sqrt{3}$,BC=$\sqrt{6}$,求∠BCD的三个角函数值.