题目内容
17.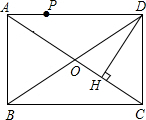 如图,点P是矩形ABCD所得边AD上的一个动点.DH⊥AC于H,那么点P到矩形的两条对角线AC和BD的距离之和等于( )
如图,点P是矩形ABCD所得边AD上的一个动点.DH⊥AC于H,那么点P到矩形的两条对角线AC和BD的距离之和等于( )| A. | 2DH | B. | $\frac{3}{2}DH$ | C. | DH | D. | $\frac{2}{3}DH$ |
分析 首先连接OP,由S△AOD=S△AOP+S△DOP和矩形的性质即可求得答案.
解答  解:连接OP,
解:连接OP,
∵PE、PF分别是点P到矩形的两条对角线AC和BD的距离,
∴S△AOP=$\frac{1}{2}$OA•PE,S△DOP=$\frac{1}{2}$OD•PF,
∵S△AOD=S△AOP+S△DOP,
∴$\frac{1}{2}$OA•PE+$\frac{1}{2}$OD•PF=$\frac{1}{2}$OA•DH,
∵四边形ABCD是矩形,
∴OA=OD,
∴PE+PF=DH,
故选C.
点评 此题考查了矩形的性质以及三角形面积问题.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
7.一条河的水流速度是1.5km/h,某船在静水中的速度是vkm/h,则该船在这条河中逆流行驶的速度正确的是( )
| A. | (v+1.5)km/h | B. | (v-1.5)km/h | C. | (v+3)km/h | D. | (v-3)km/h |
8. 如图,在数轴上点P的位置被一滴墨水遮挡了,那么请估计数轴上点P表示的数可能是( )
如图,在数轴上点P的位置被一滴墨水遮挡了,那么请估计数轴上点P表示的数可能是( )
 如图,在数轴上点P的位置被一滴墨水遮挡了,那么请估计数轴上点P表示的数可能是( )
如图,在数轴上点P的位置被一滴墨水遮挡了,那么请估计数轴上点P表示的数可能是( )| A. | -2.6 | B. | -1.4 | C. | 2.6 | D. | 1.4 |
7.在比例尺为1:10000的地图上,相距4cm的A、B两地的实际距离是( )
| A. | 400m | B. | 400dm | C. | 400cm | D. | 400km |
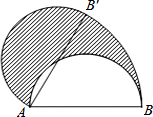 如图,直径AB为4的半圆,绕A点逆时针旋转60°,此时点B到了点B′,则图中阴影部分的面积是$\frac{8π}{3}$.
如图,直径AB为4的半圆,绕A点逆时针旋转60°,此时点B到了点B′,则图中阴影部分的面积是$\frac{8π}{3}$. =0,
=0, =4,
=4, =-7,按此规律,计算
=-7,按此规律,计算 =18.
=18.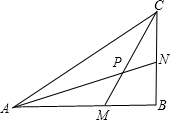 如图,在△ABC中,∠B=90°,M为AB上一点,使得AM=BC,N为BC上一点,使得CN=BM,连接AN,CM交于P点,求证:∠APM=45°.
如图,在△ABC中,∠B=90°,M为AB上一点,使得AM=BC,N为BC上一点,使得CN=BM,连接AN,CM交于P点,求证:∠APM=45°. 在平面直角坐标系中,已知抛物线与直线的图象如图所示,当y1≠y2时,取y1,y2中的较大值记为N;当y1=y2时,N=y1=y2.则下列说法:
在平面直角坐标系中,已知抛物线与直线的图象如图所示,当y1≠y2时,取y1,y2中的较大值记为N;当y1=y2时,N=y1=y2.则下列说法: 如图,OP平分∠MON,PE⊥OM于E,PF⊥ON于F,OA=OB,则图中有3对全等三角形,选择其中一对全等三角形加以证明.
如图,OP平分∠MON,PE⊥OM于E,PF⊥ON于F,OA=OB,则图中有3对全等三角形,选择其中一对全等三角形加以证明.