题目内容
6. 如图,OP平分∠MON,PE⊥OM于E,PF⊥ON于F,OA=OB,则图中有3对全等三角形,选择其中一对全等三角形加以证明.
如图,OP平分∠MON,PE⊥OM于E,PF⊥ON于F,OA=OB,则图中有3对全等三角形,选择其中一对全等三角形加以证明.
分析 根据全等三角形的判定方法我们可以得到图中共有三对全等三角形分别为:△AOP≌△BOP,△AEP≌△BFP,△OEP≌△OFP.
解答 解:图中有三对全等三角形:△AOP≌△BOP,△AEP≌△BFP,△OEP≌△OFP;
证明△OEP≌△OFP.
∵OP平分∠MON,PE⊥OM于E,PF⊥ON于F,
∴EP=FP,
在△OEP与△OFP中,
$\left\{\begin{array}{l}{EP=FP}\\{OP=OP}\end{array}\right.$,
∴△OEP≌△OFP(HL),
故答案为:3.
点评 本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
17.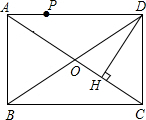 如图,点P是矩形ABCD所得边AD上的一个动点.DH⊥AC于H,那么点P到矩形的两条对角线AC和BD的距离之和等于( )
如图,点P是矩形ABCD所得边AD上的一个动点.DH⊥AC于H,那么点P到矩形的两条对角线AC和BD的距离之和等于( )
 如图,点P是矩形ABCD所得边AD上的一个动点.DH⊥AC于H,那么点P到矩形的两条对角线AC和BD的距离之和等于( )
如图,点P是矩形ABCD所得边AD上的一个动点.DH⊥AC于H,那么点P到矩形的两条对角线AC和BD的距离之和等于( )| A. | 2DH | B. | $\frac{3}{2}DH$ | C. | DH | D. | $\frac{2}{3}DH$ |
 如图,在平面直角坐标系中,将长方形AOCD沿直线AE折叠(点E在边DC上),折叠后顶点D恰好落在边OC上的点F处,若点D的坐标为(5,4),则点E的坐标为(5,$\frac{3}{2}$).
如图,在平面直角坐标系中,将长方形AOCD沿直线AE折叠(点E在边DC上),折叠后顶点D恰好落在边OC上的点F处,若点D的坐标为(5,4),则点E的坐标为(5,$\frac{3}{2}$). 如图,以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,若AC=FC.
如图,以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,若AC=FC.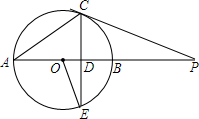 如图,AB是⊙O的直径,点P在AB的延长线上,弦CE交AB于点D,连结OE、AC,已知∠POE=2∠CAB.
如图,AB是⊙O的直径,点P在AB的延长线上,弦CE交AB于点D,连结OE、AC,已知∠POE=2∠CAB.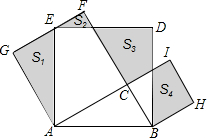 如图,Rt△ABC中,∠C=90°,AC=4,BC=3.分别以AB、AC、BC为边在AB的同侧作正方形ABDE、ACFG、BCIH,四块阴影部分的面积分别为S1、S2、S3、S4. 则S1+S2+S3+S4等于18.
如图,Rt△ABC中,∠C=90°,AC=4,BC=3.分别以AB、AC、BC为边在AB的同侧作正方形ABDE、ACFG、BCIH,四块阴影部分的面积分别为S1、S2、S3、S4. 则S1+S2+S3+S4等于18.