题目内容
19.已知直线y1=-2x+6与双曲线y2=$\frac{4}{x}$在同一坐标系的交点坐标是(1,4)和(2,2),则当y1>y2时,x的取值范围是( )| A. | x<0或1<x<2 | B. | x<1 | C. | 0<x<1或x<0 | D. | x>2 |
分析 根据直线y1=-2x+6与双曲线y2=$\frac{4}{x}$在同一坐标系的交点坐标,即可得到结论.
解答 解:∵直线y1=-2x+6与双曲线y2=$\frac{4}{x}$在同一坐标系的交点坐标是(1,4)和(2,2),
∴当y1>y2时,直线在双曲线上面,
∴当y1>y2时,x的取值范围是x<0或1<x<2,
故选A.
点评 本题考查的是反比例函数与一次函数的交点问题,解答此题的关键是利用数形结合求出x的取值范围.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
7.甲乙两人练习赛跑,甲每秒跑7米,乙每秒跑6.5米,甲让乙先跑5米,设x秒后,甲可以追上乙,则下列方程不正确结果是( )
| A. | 7x=6.5x+5 | B. | 7x-5=6.5 | C. | (7-6.5)x=5 | D. | 6.5x=7x-5 |
9.下列叙述,其中不正确的是( )
| A. | 两点确定一条直线 | |
| B. | 过一点有且只有一条直线与已知直线平行 | |
| C. | 同角(或等角)的余角相等 | |
| D. | 两点之间的所有连线中,线段最短 |
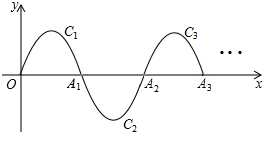 一段抛物线:y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…若P(2015,m)是其中某段抛物线上一点,则m=-2.
一段抛物线:y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…若P(2015,m)是其中某段抛物线上一点,则m=-2.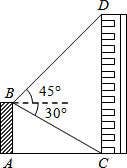 如图,在一竖直平台AB的点B处,测得楼房CD顶部点D的仰角为45°,底部点C的俯角为30°.已知楼高100米,求平台的高度.
如图,在一竖直平台AB的点B处,测得楼房CD顶部点D的仰角为45°,底部点C的俯角为30°.已知楼高100米,求平台的高度. 如图,梯子AB斜靠在一竖直的墙上,梯子的底端A到墙根O的距离AO为2米,梯子的顶端B到地面的距离BO为6米,现将梯子的底端A向外移动到A′,使梯子的底端A′到墙根O的距离A′O等于3米,同时梯子的顶端B下降至B′.求梯子顶端下滑的距离BB′.
如图,梯子AB斜靠在一竖直的墙上,梯子的底端A到墙根O的距离AO为2米,梯子的顶端B到地面的距离BO为6米,现将梯子的底端A向外移动到A′,使梯子的底端A′到墙根O的距离A′O等于3米,同时梯子的顶端B下降至B′.求梯子顶端下滑的距离BB′. 已知函数y=mx+n和y=$\frac{1}{2}x$的图象交于点P(a,-2),则二元一次方程组$\left\{\begin{array}{l}{y=mx+n}\\{y=\frac{1}{2}x}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=-4}\\{y=-2}\end{array}\right.$.
已知函数y=mx+n和y=$\frac{1}{2}x$的图象交于点P(a,-2),则二元一次方程组$\left\{\begin{array}{l}{y=mx+n}\\{y=\frac{1}{2}x}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=-4}\\{y=-2}\end{array}\right.$. 如图,在由相同的小正方形组成的网格线上,点A,B,C,D都在这些小正方形的顶点,AB、CD相交于点P,求BP:PE:AE的值.
如图,在由相同的小正方形组成的网格线上,点A,B,C,D都在这些小正方形的顶点,AB、CD相交于点P,求BP:PE:AE的值. 如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )