Question

10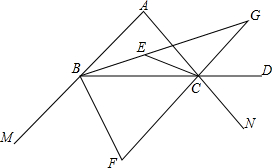．在△ABC中，BG平分∠ABC，CE平分∠ACB，CG，BF，CF分别是△ABC的外角的角平分线，已知∠A=70°．
（1）求∠BEC，∠F，∠G的度数．
（2）△BFG和△CEG有何共同的特点？
（3）无论∠A为何度数，∠BEC和∠F有何数量关系？∠G和∠F有何数量关系？

Answer 1

分析 （1）根据三角形的内角和得到∠ABC+∠ACB=180°-70°=110°，由角平分线的性质得到∠1+∠2=$\frac{1}{2}$（∠ABC+∠ACB）=55°，根据三角形的内角和得到∠BEC=180°-∠1-∠2=125°，根据角平分线和平角的定义得到∠1+∠3=∠2+∠4=90°，根据四边形的内角和即可得到结果；
（2）根据角平分线的性质和平角的定义即可得到结论；
（3）由（1）知，∠GBF=∠ECF=90°，根据四边形的内角和即可得到结论．

解答 解：（1）∵∠A=70°，
∴∠ABC+∠ACB=180°-70°=110°，
∵BG平分∠ABC，CE平分∠ACB，
∴∠1+∠2=$\frac{1}{2}$（∠ABC+∠ACB）=55°，
∴∠BEC=180°-∠1-∠2=125°，
∵BF平分∠MBC，CF平分∠BCN，
∴∠1+∠3=∠2+∠4=90°，
∴∠F=360°-90°-90°-125°=55°，
∴∠G=90°-∠F=35°；

（2）∵CG平分∠ACD，
∴∠2+∠5=90°，
∴∠ECG=90°，
∴△BFG和△CEG是直角三角形；

（3）由（1）知，∠GBF=∠ECF=90°，
∴∠BEC+∠F=360°-90°-90°=180°．
∴∠G+∠F=90°，
∴不论∠A为何度数，∠BEC和∠F互补，∠G和∠F互余．

点评 本题考查了三角形的内角和，三角形外角的性质，四边形的内角和，平角的定义，熟练掌握各性质定理是解题的关键．