题目内容
16.定义:若函数y1与y2同时满足下列两个条件:①两个函数的自变量x,都满足a≤x≤b;
②在自变量范围内对于任意的x1都存在x2,使得x1所对应的函数值y1与x2所对应的函数值y2相等. 我们就称y1与y2这两个函数为“兄弟函数”.
设函数y1=x2-2x-3,y2=kx-1
(1)当k=-1时,求出所有使得y1=y2成立的x值;
(2)当1≤x≤3时判断函数y1=$\frac{3}{x}$与y2=-x+5是不是“兄弟函数”,并说明理由;
(3)已知:当-1≤x≤2时函数y1=x2-2x-3与y2=kx-1是“兄弟函数”,试求实数k的取值范围?
分析 (1)将k=-1代入一次函数,与二次函数联立方程组,求出方程组的解即为x的值;
(2)假设两个函数是兄弟函数,联立方程组,求出x的值,判断x值是否符合相应取值范围,经过判断,两个函数不是兄弟函数;
(3)利用兄弟函数的定义,联立函数解析式,求出x的值,然后将x的值带入x的取值范围,得到一个不等式组,解不等式组即可.
解答 解:(1)当k=-1时,y2=-x-1,
根据题意得:x2-2x-3=-x-1,
解得:x=2或x=-1;
∴x的 值为2或-1.
(2)不是
若$\frac{3}{x}$=-x+5,
则x2-5x+3=0,
解得:x=$\frac{5±\sqrt{13}}{2}$,
∵3<$\sqrt{13}$<4
∴4<$\frac{5+\sqrt{13}}{2}$<$\frac{9}{2}$,$\frac{1}{2}$<$\frac{5-\sqrt{13}}{2}$<1,
两根均不在1≤x≤3,
∴函数y1=$\frac{3}{x}$与y2=-x+5不是“兄弟函数”.
(3)∵函数y1=x2-2x-3与y2=kx-1是“兄弟函数”,
∴x2-2x-3=kx-1,
整理得:x2-(2+k)x-2=0,
解得:x=$\frac{2+k±\sqrt{(2+k)^{2}+8}}{2}$,
∵-1≤x≤2时函数y1=x2-2x-3与y2=kx-1是“兄弟函数”,
∴-1≤$\frac{2+k+\sqrt{(2+k)^{2}+}8}{2}$≤2,
解得:k≤-3,
或1≤$\frac{2+k-\sqrt{(2+k)^{2}+}8}{2}$≤2,
解得:k≥-1.
∴实数k的取值范围:k≤-3或k≥-1.
点评 题目考查了兄弟函数的定义,属于新定义类型,在考查新定义的同时,考查一次函数、二次函数、反比例函数的性质,运用联立方程求出方程的根.题目整体较难,在理解的同时,考查学生快速理解新定义的能力,这也是中考变革的方向.

| A. | 一个角的补角比它的余角大 | B. | 若两角相等,则它们的补角也相等 | ||
| C. | 相等的角是对顶角 | D. | 两个钝角不能互补 |
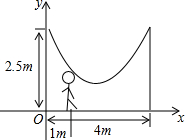 如图,小明的爸爸在相距4m的两树等高位置处拴了一根绳子,做成一个简易的秋千,绳子自然下垂呈抛物线,已知身高1.5m的小明站在距离树1m的地方,头部刚好触到绳子.
如图,小明的爸爸在相距4m的两树等高位置处拴了一根绳子,做成一个简易的秋千,绳子自然下垂呈抛物线,已知身高1.5m的小明站在距离树1m的地方,头部刚好触到绳子. 如图,山脚下有一棵树AB,小强从点B沿山坡向上走50m到达点D,用高为1.5m的测角仪CD测得树顶为10°,已知山坡的坡脚为15°,则树AB的高=23.2m(精确到0.1m)(已知sin10°≈0.17,cos10°≈0.98,tan10°≈0.18,sin15°≈0.26,cos15°≈0.97,tan15°≈0.27).
如图,山脚下有一棵树AB,小强从点B沿山坡向上走50m到达点D,用高为1.5m的测角仪CD测得树顶为10°,已知山坡的坡脚为15°,则树AB的高=23.2m(精确到0.1m)(已知sin10°≈0.17,cos10°≈0.98,tan10°≈0.18,sin15°≈0.26,cos15°≈0.97,tan15°≈0.27).