题目内容
18.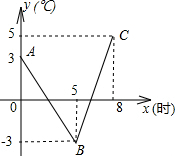 一种大棚蔬菜处在0℃以下的气温条件下超过3h,就会遭受冻害,秋末某天,该地区气象台发布如下的降温预报:由0时至次曰8时,气温y(℃)与时刻x(h)的函数关系如图中折线A-B-C所示
一种大棚蔬菜处在0℃以下的气温条件下超过3h,就会遭受冻害,秋末某天,该地区气象台发布如下的降温预报:由0时至次曰8时,气温y(℃)与时刻x(h)的函数关系如图中折线A-B-C所示(1)根据图中数值,求线段AB、BC的函数关系式(不必写自变量的取值范围);
(2)你认为是否有必要对大棚蔬菜采取防冻措施?请说明理由.
分析 (1)根据函数图象中的数据可以求得线段AB、BC的函数关系式;
(2)根据(1)中的函数解析式可以分别求BC和AB与x轴的交点,然后作差与3比较大小即可解答本题.
解答 解:(1)设线段AB对应的函数解析式为y=ax+b,
$\left\{\begin{array}{l}{b=3}\\{5a+b=-3}\end{array}\right.$,得$\left\{\begin{array}{l}{a=-1.2}\\{b=3}\end{array}\right.$,
即线段AB对应的函数解析式为y=-1.2x+3,
设线段BC对应的函数解析式为y=cx+d,
$\left\{\begin{array}{l}{5c+d=-3}\\{8c+d=5}\end{array}\right.$,得$\left\{\begin{array}{l}{c=2}\\{d=-13}\end{array}\right.$,
即线段BC对应的函数解析式为y=2x-13;
(2)有必要对大棚蔬菜采取防冻措施,
理由:将y=0代入y=-1.2x+3得,x=2.5,
将y=0代入y=2x-13,得x=6.5,
∵6.6-2.5=4>3,
∴有必要对大棚蔬菜采取防冻措施.
点评 本题考查一次函数的应用,解答本题的关键是明确题意,找出所求问题需要的条件,求出相应的函数解析式,利用一次函数的性质解答.

练习册系列答案
相关题目
8.将某抛物线图象向右平移2个单位,再向下平移3个单位所得的抛物线是y=-2x2+4x+1的图象,则将该抛物线沿y轴翻折后所得的函数关系式是( )
| A. | y=-2(x-1)2+6 | B. | y=-2(x-1)2-6 | C. | y=-2(x+1)2+6 | D. | y=2(x+1)2-6 |
10.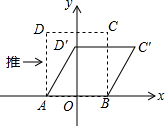 我们知道:四边形具有不稳定性.如图,在平面直角坐标系中,边长为2的正方形ABCD的边AB在x轴上,AB的中点是坐标原点O,固定点A,B,把正方形沿箭头方向推,使点D落在y轴正半轴上点D′处,则点C的对应点C′的坐标为( )
我们知道:四边形具有不稳定性.如图,在平面直角坐标系中,边长为2的正方形ABCD的边AB在x轴上,AB的中点是坐标原点O,固定点A,B,把正方形沿箭头方向推,使点D落在y轴正半轴上点D′处,则点C的对应点C′的坐标为( )
 我们知道:四边形具有不稳定性.如图,在平面直角坐标系中,边长为2的正方形ABCD的边AB在x轴上,AB的中点是坐标原点O,固定点A,B,把正方形沿箭头方向推,使点D落在y轴正半轴上点D′处,则点C的对应点C′的坐标为( )
我们知道:四边形具有不稳定性.如图,在平面直角坐标系中,边长为2的正方形ABCD的边AB在x轴上,AB的中点是坐标原点O,固定点A,B,把正方形沿箭头方向推,使点D落在y轴正半轴上点D′处,则点C的对应点C′的坐标为( )| A. | ($\sqrt{3}$,1) | B. | (2,1) | C. | (1,$\sqrt{3}$) | D. | (2,$\sqrt{3}$) |
8.为有效开展“阳光体育”活动,某校计划购买篮球和足球共50个,购买资金不超过3000元.若每个篮球80元,每个足球50元,则篮球最多可购买( )
| A. | 16个 | B. | 17个 | C. | 33个 | D. | 34个 |




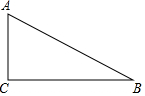 如图,已知Rt△ABC,∠C=90°,AC=3,BC=4.分别以点A、B为圆心画圆.如果点C在⊙A内,点B在⊙A外,且⊙B与⊙A内切,那么⊙B的半径长r的取值范围是8<r<10.
如图,已知Rt△ABC,∠C=90°,AC=3,BC=4.分别以点A、B为圆心画圆.如果点C在⊙A内,点B在⊙A外,且⊙B与⊙A内切,那么⊙B的半径长r的取值范围是8<r<10. 如图,BC∥EF,AC∥DF,添加一个条件AB=DE或BC=EF或AC=DF或AD=BE(只需添加一个即可),使得△ABC≌△DEF.
如图,BC∥EF,AC∥DF,添加一个条件AB=DE或BC=EF或AC=DF或AD=BE(只需添加一个即可),使得△ABC≌△DEF.