题目内容
15.射击游戏中要求参加者命中如图所示的九个铁罐之一,获奖规则如下:一等奖:命中数字“7”;二等奖:命中3的倍数;三等奖:命中奇数;四等奖:命中偶数,你觉得这样的获奖规则是否合理?为什么?你有别的建议吗?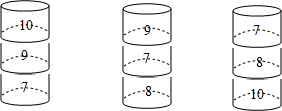
分析 分别计算出各等奖的概率,比较大小即可得到游戏规则是否合理.
解答 解:不合理,
理由如下:
∵一等奖:命中数字“7”的概率=$\frac{1}{3}$;
二等奖:命中3的倍数的概率=$\frac{2}{9}$;
三等奖:命中奇数的概率=$\frac{5}{9}$;
四等奖:命中偶数的概率=$\frac{4}{9}$,
∴各等奖的概率和=$\frac{1}{3}$+$\frac{2}{9}$+$\frac{5}{9}$+$\frac{4}{9}$>1,
∴不合理,
建议:获得三等奖的游戏规则和获得四等奖的游戏规则分别改为:命中数字“8”、命中数字“9”.
点评 本题考查的是游戏公平性的判断.判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.

练习册系列答案
相关题目
5.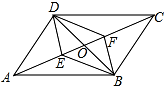 如图,在平行四边形ABCD中,对角线AC、BD相交于点O,E、F是对角线AC上的两点,给出下列四个条件:①AE=CF;②DE=BF;③∠ADE=∠CBF;④∠ABE=∠CDF.其中不能判定四边形DEBF是平行四边形的有( )
如图,在平行四边形ABCD中,对角线AC、BD相交于点O,E、F是对角线AC上的两点,给出下列四个条件:①AE=CF;②DE=BF;③∠ADE=∠CBF;④∠ABE=∠CDF.其中不能判定四边形DEBF是平行四边形的有( )
 如图,在平行四边形ABCD中,对角线AC、BD相交于点O,E、F是对角线AC上的两点,给出下列四个条件:①AE=CF;②DE=BF;③∠ADE=∠CBF;④∠ABE=∠CDF.其中不能判定四边形DEBF是平行四边形的有( )
如图,在平行四边形ABCD中,对角线AC、BD相交于点O,E、F是对角线AC上的两点,给出下列四个条件:①AE=CF;②DE=BF;③∠ADE=∠CBF;④∠ABE=∠CDF.其中不能判定四边形DEBF是平行四边形的有( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
20.某次歌唱比赛,最后三名选手的成绩统计如表:
(1)若按算术平均分排出冠军、亚军、季军,则冠军、亚军、季军各是谁?
(2)若按6:3:1的加权平均分排出冠军、亚军、季军,则冠军、亚军、季军各是谁?
(3)若最后排名冠军是王晓丽,亚军是李真,季军是林飞扬,则权重可能是多少?
| 比赛项目 | 比赛成绩/分 | ||
| 王晓丽 | 李真 | 林飞扬 | |
| 唱功 | 98 | 95 | 80 |
| 音乐常识 | 80 | 90 | 100 |
| 综合知识 | 80 | 90 | 100 |
(2)若按6:3:1的加权平均分排出冠军、亚军、季军,则冠军、亚军、季军各是谁?
(3)若最后排名冠军是王晓丽,亚军是李真,季军是林飞扬,则权重可能是多少?
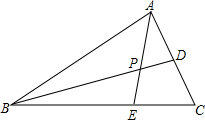 如图,在△ABC中,点D、E分别在AC、BC边上,且AD=CD,BE=2CE,AE与BD交于P点.若△ABC的面积为1,求四边形CDPE的面积.
如图,在△ABC中,点D、E分别在AC、BC边上,且AD=CD,BE=2CE,AE与BD交于P点.若△ABC的面积为1,求四边形CDPE的面积.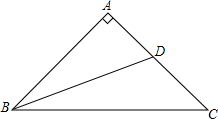 如图,已知在Rt△ABC中,∠A=90°,AB=BC,BD是AC边上的中线,求cot∠DBC.
如图,已知在Rt△ABC中,∠A=90°,AB=BC,BD是AC边上的中线,求cot∠DBC.