题目内容
 如图在梯形ABCD中,AD∥BC,AB=AD=DC,AC⊥AB,将CB延长至点F,使BF=CD.求∠CAF的度数.
如图在梯形ABCD中,AD∥BC,AB=AD=DC,AC⊥AB,将CB延长至点F,使BF=CD.求∠CAF的度数.
分析:首先由AD=DC与AD∥BC,根据平行线与等腰三角形的性质,即可求得∠DCA=∠ACB,又由等腰梯形的性质,求得∠ABC=2∠ACB,由AC⊥AB,即可求得∠ABC的度数,然后由AB=BF,根据等边对等角的知识,求得∠BAF的度数,则可求得∠CAF的度数.
解答:解:∵AD∥BC,
∴∠DAC=∠ACB,
∵AD=DC,
∴∠DCA=∠DAC,
∴∠ACD=∠ACB=
∠DCB,
∵AB=DC,
∴∠ABC=∠DCB=2∠ACB,
∵AC⊥AB,
∴∠CAB=90°,
∴∠ABC=60°,
∵AB=BF,
∴∠BAF=∠F,
∵∠ABC=∠BAF+∠F,
∴∠BAF=30°,
∴∠CAF=∠CAB+∠BAF=90°+30°=120°.
∴∠DAC=∠ACB,
∵AD=DC,
∴∠DCA=∠DAC,
∴∠ACD=∠ACB=
| 1 |
| 2 |
∵AB=DC,
∴∠ABC=∠DCB=2∠ACB,
∵AC⊥AB,
∴∠CAB=90°,
∴∠ABC=60°,
∵AB=BF,
∴∠BAF=∠F,
∵∠ABC=∠BAF+∠F,
∴∠BAF=30°,
∴∠CAF=∠CAB+∠BAF=90°+30°=120°.
点评:此题考查了等腰梯形、等腰三角形以及平行线的性质.此题难度适中,解题的关键是注意数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图在梯形ABCD中,AB=DC=10cm,AC与BD相交于G,且∠AGD=60°,设E为CG的中点,F为AB的中点,则EF的长为
如图在梯形ABCD中,AB=DC=10cm,AC与BD相交于G,且∠AGD=60°,设E为CG的中点,F为AB的中点,则EF的长为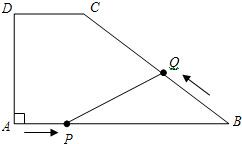 发以3厘米/秒的速度沿B?C?D方向向点D运动,两个动点同时出发,当其中一个动点到达终点时,另一个动点也随之停止.设动点运动的时间为t秒.
发以3厘米/秒的速度沿B?C?D方向向点D运动,两个动点同时出发,当其中一个动点到达终点时,另一个动点也随之停止.设动点运动的时间为t秒. 如图在梯形ABCD中,AD∥BC,E是梯形内一点,ED⊥AD,∠EBC=∠EDC,∠ECB=45°.
如图在梯形ABCD中,AD∥BC,E是梯形内一点,ED⊥AD,∠EBC=∠EDC,∠ECB=45°. (2011•宣城模拟)我们知道连接三角形两边中点的线段叫做三角形的中位线;通过证明可以得到“三角形的中位线平行于三角形的第三边,且等于第三边的一半”类似三角形中位线,我们把连接梯形两腰中点的线段叫做梯形的中位线.如图在梯形ABCD中,AD∥BC,点E,F分别是AB、CD的中点,观察EF的位置,联想三角形中位线的性质,你能发现梯形的中位线有什么性质?证明你的结论.
(2011•宣城模拟)我们知道连接三角形两边中点的线段叫做三角形的中位线;通过证明可以得到“三角形的中位线平行于三角形的第三边,且等于第三边的一半”类似三角形中位线,我们把连接梯形两腰中点的线段叫做梯形的中位线.如图在梯形ABCD中,AD∥BC,点E,F分别是AB、CD的中点,观察EF的位置,联想三角形中位线的性质,你能发现梯形的中位线有什么性质?证明你的结论. 如图在梯形ABCD中,AD∥BC,∠B=∠C,DE交BC于点E,AD=BE.
如图在梯形ABCD中,AD∥BC,∠B=∠C,DE交BC于点E,AD=BE.