题目内容
3.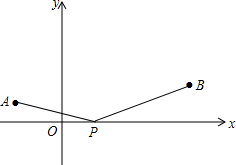 如图,点A、B的坐标分别为(-1,1),(3,2),P为x轴上一点,求当BP-AP最大时和当BP+AP最小时,求P点的坐标.
如图,点A、B的坐标分别为(-1,1),(3,2),P为x轴上一点,求当BP-AP最大时和当BP+AP最小时,求P点的坐标.
分析 ①连接AB,则AB与x轴的交点P即为所求的点,用待定系数法求出AB所在直线的解析式,再根据x轴上点的坐标特点求出P点坐标即可;
②作点B关于x轴的对称点B′(3,-2),连接AB′交x轴于P′,则AP′+B′P′=AP′+BP′最小,用待定系数法求出AB所在直线的解析式,再根据x轴上点的坐标特点求出P点坐标即可.
解答 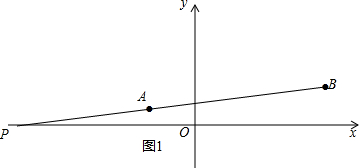 解:①如图1,连接BA交x轴与P,则PB-PA=AB值最大,
解:①如图1,连接BA交x轴与P,则PB-PA=AB值最大,
设直线AB的解析式为y=kx+b,
∴$\left\{\begin{array}{l}{1=-k+b}\\{2=3k+b}\end{array}\right.$,∴$\left\{\begin{array}{l}{k=\frac{1}{4}}\\{b=\frac{5}{4}}\end{array}\right.$,
∴直线AB的解析式为y=$\frac{1}{4}$x+$\frac{5}{4}$,
当y=0时,即$\frac{1}{4}$x+$\frac{5}{4}$=0,
∴x=-5,
∴P(-5,0);
②如图2,作点B关于x轴的对称点B′(3,-2),连接AB′交x轴于P′,则AP′+B′P′=AP′+BP′最小,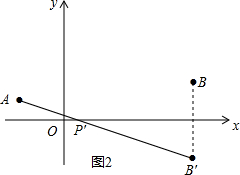
设直线AB′的解析式为y=mx+n,
∴$\left\{\begin{array}{l}{1=-m+n}\\{-2=3m+n}\end{array}\right.$,∴$\left\{\begin{array}{l}{m=-\frac{3}{4}}\\{n=\frac{1}{4}}\end{array}\right.$,
∴直线AB′的解析式为y=-$\frac{3}{4}$x+$\frac{1}{4}$,
当y=0时,即-$\frac{3}{4}$x+$\frac{1}{4}$=0,
∴x=$\frac{1}{3}$,
∴P′($\frac{1}{3}$,0).
点评 本题考查了轴对称-最短线路问题及用待定系数法求一次函数的解析式,是一道综合性题目.

 核心素养学练评系列答案
核心素养学练评系列答案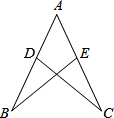 如图,已知AD=AE,BD=CE,求证:△ABE≌△ACD.
如图,已知AD=AE,BD=CE,求证:△ABE≌△ACD.
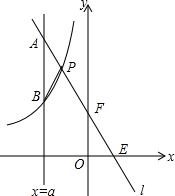 如图,一次函数y=k1x+b的图象l与坐标轴分别交于点E、F,与双曲线y=-$\frac{{k}_{2}}{x}$(x<0)交于点P(-1,4),且F是PE的中点.
如图,一次函数y=k1x+b的图象l与坐标轴分别交于点E、F,与双曲线y=-$\frac{{k}_{2}}{x}$(x<0)交于点P(-1,4),且F是PE的中点.
 如图,在梯形ABCD中,AD∥BC,对角线AC⊥BD且AC=12,BD=5,则梯形的高DE=$\frac{60}{13}$.
如图,在梯形ABCD中,AD∥BC,对角线AC⊥BD且AC=12,BD=5,则梯形的高DE=$\frac{60}{13}$.