题目内容
如图14,已知CD是⊙O的直径,点A为CD延长线上一点,BC=AB,∠CAB=30°.
(1)求证:AB是⊙O的切线;
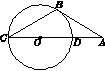
图14
(2)若⊙O的半径为2,求⌒BD的长.
(1)证明:连接OB,如答图6所示:

答图6
∵BC=AB,∠CAB=30°,
∴∠ACB=∠CAB=30°,
又∵OC=OB,
∴∠CBO=∠ACB=30°,
∴∠AOB=∠CBO+∠ACB=60°.
在△ABO中,∠CAB=30°,∠AOB=60°,
可得∠ABO=90°,即AB⊥OB,
∴AB是⊙O的切线.
(2)解:∵OB=2,∠BOD=60°,
∴⌒BD的长度l= π.
π.
点拨:此题考查了切线的判定,等腰三角形的性质,三角形的外角性质以及弧长公式的运用.切线的判定方法有两种:有切点连半径,证明垂直;无切点作垂线,证明垂线段等于半径.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目

 aπ
aπ

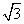 a B.b=
a B.b=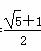 a C.b=
a C.b=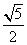 a D. b=
a D. b= a
a