题目内容
18．下面各对数中互为相反数的是（ ）| A． | （-3）2与-32 | B． | （-2）3与-23 | C． | -22与32 | D． | （-3×2）2与-3×22 |
分析 根据有理数的乘方和相反数的定义对各选项分析判断即可得解．
解答 解：A、（-3）2=9，-32=-9，是互为相反数，故本选项正确；
B、（-2）3=-8，-23=-8，不是互为相反数，故本选项错误；
C、-22=-4，32=9，不是互为相反数，故本选项错误；
D、（-3×2）2=36，-3×22=-12，不是互为相反数，故本选项错误．
故选A．
点评 本题考查了有理数的乘方，相反数的定义，有理数的乘法，熟记概念并准确计算是解题的关键，计算时要注意运算符号的处理．
练习册系列答案
名校课堂系列答案
相关题目
8．a4+a4的结果是（ ）
| A． | a8 | B． | 2a8 | C． | a16 | D． | 2a4 |
9．下列点中在反比例函数y=$\frac{2}{x}$图象上的是（ ）
| A． | （-2，1） | B． | （1，-2） | C． | （-2，-2） | D． | （1，2） |
6．下列解方程过程中，变形正确的是（ ）
| A． | 由x+5=6x-7得5x=5-7 | B． | 由-2（x-1）=3得-2x-2=3 | ||
| C． | 由$\frac{x-3}{0.7}$=1得$\frac{10x-30}{7}$=10 | D． | 由$\frac{1}{2}$x+9=-$\frac{3}{2}$x-3得2x=-12 |
13．若关于x的不等式组$\left\{\begin{array}{l}{\frac{x+15}{2}＞x-3}\\{\frac{2x+2}{3}＜x+a}\end{array}\right.$的解只有4个整数解，则a的取值范围是（ ）
| A． | -$\frac{14}{3}$＜a＜-5 | B． | -5≤a＜-$\frac{14}{3}$ | C． | -5＜a≤-$\frac{14}{3}$ | D． | -$\frac{14}{3}$＜a≤-5 |
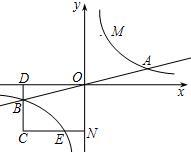已知双曲线y=$\frac{k}{x}$与直线y=$\frac{1}{4}$x相交于A、B两点，第一象限上的点M（m，n）（在A点左侧）是双曲线的动点，过点B作BD∥于y轴于点D，过N（-，-n）作NC∥x轴交双曲线于点E，交BD于点C．若B是CD的中点，四边形OBCE的面积为4，则直线CM的解析式为y=$\frac{2}{3}$x+$\frac{2}{3}$．
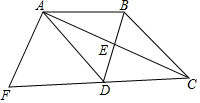如图，四边形ABCD中，BD垂直平分AC，垂足为点E，点F为四边形ABCD外一点，DA平分∠BDF，∠ADF=∠BAD，且AF⊥AC．