题目内容
8.已知点D在AB上,点E在AC上,AB=AC,∠ABE=∠ACD.(1)如图①,求证:AD=AE.
(2)如图②,若BE、CD交于点P,连接BC,求证:PB=PC.
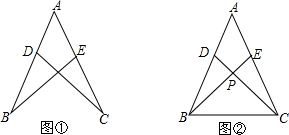
分析 (1)利用ASA证明△ABE≌△ACD,根据全等三角形的对应边相等即可解答;
(2)根据AB=AC(等角对等边),得到∠ABC=∠ACB,由∠ABE=∠ACD,得到∠PBC=∠PCB,即可解答.
解答 解:(1)在△ABE和△ACD中,
$\left\{\begin{array}{l}{∠A=∠A}\\{AB=AC}\\{∠ABE=∠ACD}\end{array}\right.$,
∴△ABE≌△ACD(ASA),
∴AD=AE.
(2)∵AB=AC,
∴∠ABC=∠ACB,
∵∠ABE=∠ACD,
∴∠ABC-∠ABE=∠ACB-∠ACD,
∴∠PBC=∠PCB,
∴PB=PC.
点评 本题考查了全等三角形的性质与判定,熟练应用全等三角形的判定方法是解决本题的关键.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
19.下列式子中,正确的是( )
①-|-5|=-5;②|-(-5)|=-5;③-(-5)=-5;④-[-(-5)]=-5.
①-|-5|=-5;②|-(-5)|=-5;③-(-5)=-5;④-[-(-5)]=-5.
| A. | ①和② | B. | ①和③ | C. | ①和④ | D. | ②和③ |
3.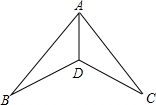 如图,下列条件中,不能证明△ABD≌△ACD的是( )
如图,下列条件中,不能证明△ABD≌△ACD的是( )
 如图,下列条件中,不能证明△ABD≌△ACD的是( )
如图,下列条件中,不能证明△ABD≌△ACD的是( )| A. | ∠B=∠C,BD=DC | B. | BD=DC,AB=AC | C. | ∠B=∠C,∠BAD=∠CAD | D. | ∠ADB=∠ADC,BD=DC |
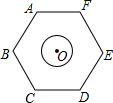 如图,圆心O恰好为正六边形ABCDEF的中心,已知AB=2$\sqrt{3}$,⊙O的半径为1,现将⊙O在正六边形内部沿某一方向平移,当它与正六边形ABCDEF的某条边相切时停止平移,设此时平移的距离为d,则d的取值范围是2≤d≤$\frac{4\sqrt{3}}{3}$.
如图,圆心O恰好为正六边形ABCDEF的中心,已知AB=2$\sqrt{3}$,⊙O的半径为1,现将⊙O在正六边形内部沿某一方向平移,当它与正六边形ABCDEF的某条边相切时停止平移,设此时平移的距离为d,则d的取值范围是2≤d≤$\frac{4\sqrt{3}}{3}$.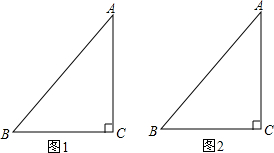 已知△ABC,∠C=90°,AC=4,BC=3.
已知△ABC,∠C=90°,AC=4,BC=3.