题目内容
 如图,在△ABC中,∠ABC=50°,∠ACB=80°,延长CB至D,使DB=BA,延长BC至E,使CE=CA,连接AD,AE.求∠D,∠E,∠DAE的度数.
如图,在△ABC中,∠ABC=50°,∠ACB=80°,延长CB至D,使DB=BA,延长BC至E,使CE=CA,连接AD,AE.求∠D,∠E,∠DAE的度数.考点:等腰三角形的性质
专题:
分析:由题意知△ABD和△ACE均为等腰三角形,可由三角形内角和定理求得∠BAC的度数,用三角形的外角与内角的关系求得∠D与∠E的度数,即可求得∠DAE的度数.
解答:解:∵∠ABC=50°,∠ACB=80°,
∴∠BAC=180°-∠ABC-∠ACB=180°-50°-80°=50°,
∵DB=BA,
∴∠D=∠DAB=
∠ABC=25°,
∵CE=CA,
∴∠E=∠CAE=
∠ACB=40°,
∴∠DAE=∠DAB+∠BAC+∠CAE=25°+50°+40°=115°.
∴∠BAC=180°-∠ABC-∠ACB=180°-50°-80°=50°,
∵DB=BA,
∴∠D=∠DAB=
| 1 |
| 2 |
∵CE=CA,
∴∠E=∠CAE=
| 1 |
| 2 |
∴∠DAE=∠DAB+∠BAC+∠CAE=25°+50°+40°=115°.
点评:本题考查的是等腰三角形的性质,熟知等边对等角、三角形的外角与内角的关系、三角形的内角和定理是正确解答本题的关键.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
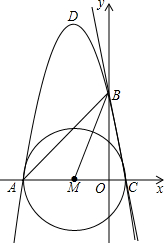 如图,已知抛物线y=-x2-4x+k的图象,与x轴交于A,C两点,与y轴交于点B(0,5),点M(a,0)在x轴上运动.
如图,已知抛物线y=-x2-4x+k的图象,与x轴交于A,C两点,与y轴交于点B(0,5),点M(a,0)在x轴上运动. (1)请把图中的四边形ABCD先向左平移6个单位,再向下平移8个单位,画出平移后的四边形,并指出四边形ABCD中各顶点的坐标;
(1)请把图中的四边形ABCD先向左平移6个单位,再向下平移8个单位,画出平移后的四边形,并指出四边形ABCD中各顶点的坐标;