题目内容
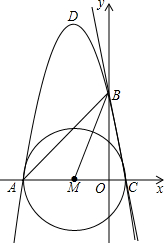 如图,已知抛物线y=-x2-4x+k的图象,与x轴交于A,C两点,与y轴交于点B(0,5),点M(a,0)在x轴上运动.
如图,已知抛物线y=-x2-4x+k的图象,与x轴交于A,C两点,与y轴交于点B(0,5),点M(a,0)在x轴上运动.(1)求k的值.
(2)当△ABM为等腰三角形时,求点M的坐标.
(3)当a为何值时,以AC的长为直径的⊙M与直线BC相切,并说明理由.
考点:二次函数综合题
专题:
分析:(1)直接利用B(0,5),代入解析式求出即可;
(2)利用等腰三角形的性质分别以AB为底边以及AB为腰,求出即可;
(3)当⊙M于直线BC相切时,设切点为E,连结ME,利用相似三角形的判定与性质得出a的值即可.
(2)利用等腰三角形的性质分别以AB为底边以及AB为腰,求出即可;
(3)当⊙M于直线BC相切时,设切点为E,连结ME,利用相似三角形的判定与性质得出a的值即可.
解答: 解:(1)把点B(0,5)代入y=-x2-4x+k
解:(1)把点B(0,5)代入y=-x2-4x+k
得 k=5;
(2)①以AB为底边,
∵y=-x2-4x+5,
当y=0,解得:x1=1,x2=-5,
∴AO=5,
∴AB=5
,
AO=BO=5,
则点M的坐标为(0,0),
②以AB为腰,AB=BM或AB=AM,则点M的坐标为(5,0)或(-5-5
,0)或(0,-5)或(5
-5,0);
(3)根据题意得出:AC=6,C(1,0),BC=
,
当⊙M于直线BC相切时,设切点为E,连结ME,
则△MCE∽△BOC,
∴
=
,
∴
=
,
∴MC=
,
∴MO=
-1,
∴a=-
+1,
同理可得:当⊙M的圆心在y轴右侧,则a=
+1,
综上所述:当a=-
+1或
+1时,以AC的长为直径的⊙M与直线BC相切.
 解:(1)把点B(0,5)代入y=-x2-4x+k
解:(1)把点B(0,5)代入y=-x2-4x+k得 k=5;
(2)①以AB为底边,
∵y=-x2-4x+5,
当y=0,解得:x1=1,x2=-5,
∴AO=5,
∴AB=5
| 2 |
AO=BO=5,
则点M的坐标为(0,0),
②以AB为腰,AB=BM或AB=AM,则点M的坐标为(5,0)或(-5-5
| 2 |
| 2 |
(3)根据题意得出:AC=6,C(1,0),BC=
| 26 |
当⊙M于直线BC相切时,设切点为E,连结ME,
则△MCE∽△BOC,
∴
| MC |
| ME |
| BC |
| BO |
∴
| MC |
| 3 |
| ||
| 5 |
∴MC=
3
| ||
| 5 |
∴MO=
3
| ||
| 5 |
∴a=-
3
| ||
| 5 |
同理可得:当⊙M的圆心在y轴右侧,则a=
3
| ||
| 5 |
综上所述:当a=-
3
| ||
| 5 |
3
| ||
| 5 |
点评:此题主要考查了二次函数综合以及相似三角形的判定与性质等知识,利用分类讨论得出是解题关键.

练习册系列答案
相关题目
①两个符号相反的分数之间至少有一个正整数;
②两个符号相反的分数之间至少有一个负整数;
③两个符号相反的分数之间至少有一个整数;
④两个符号相反的分数之间至少有一个无限不循环小数.
说法中正确的有( )个.
②两个符号相反的分数之间至少有一个负整数;
③两个符号相反的分数之间至少有一个整数;
④两个符号相反的分数之间至少有一个无限不循环小数.
说法中正确的有( )个.
| A、1个 | B、2个 | C、3个 | D、4个 |
下面四个实数中,是无理数的为( )
| A、-3 | ||
| B、0 | ||
C、
| ||
D、
|
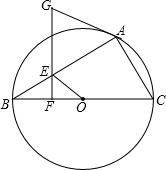 如图,已知,⊙O为△ABC的外接圆,BC为直径,点E在AB上,过点E作EF⊥BC,点G在FE的延长线上,且GA=GE.
如图,已知,⊙O为△ABC的外接圆,BC为直径,点E在AB上,过点E作EF⊥BC,点G在FE的延长线上,且GA=GE. 如图,在△ABC中,∠ABC=50°,∠ACB=80°,延长CB至D,使DB=BA,延长BC至E,使CE=CA,连接AD,AE.求∠D,∠E,∠DAE的度数.
如图,在△ABC中,∠ABC=50°,∠ACB=80°,延长CB至D,使DB=BA,延长BC至E,使CE=CA,连接AD,AE.求∠D,∠E,∠DAE的度数.