题目内容
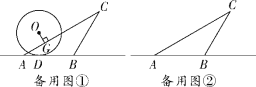
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,半径为2的
,半径为2的![]() 从点
从点![]() 开始(如图①)沿直线
开始(如图①)沿直线![]() 向右滚动,滚动时始终与直线
向右滚动,滚动时始终与直线![]() 相切(切点为
相切(切点为![]() ),当
),当![]() 与
与![]() 只有一个公共点时滚动停止.作
只有一个公共点时滚动停止.作![]() 于点
于点![]() .
.
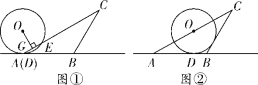
(1)图①中,![]() 在
在![]() 边上截得的弦长
边上截得的弦长![]() ______;
______;
(2)当圆心落在![]() 上时,如图②,判断
上时,如图②,判断![]() 与
与![]() 的位置关系,请说明理由;
的位置关系,请说明理由;
(3)在![]() 滚动过程中,线段
滚动过程中,线段![]() 的长度随之变化,设
的长度随之变化,设![]() ,
,![]() ,求出
,求出![]() 与
与![]() 之间的函数关系式,并直接写出
之间的函数关系式,并直接写出![]() 的取值范围.
的取值范围.
【答案】(1)2;(2)![]() 与
与![]() 相切,详见解析;(3)
相切,详见解析;(3)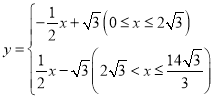
【解析】
(1)要求![]() 的长度,需做辅助线构造
的长度,需做辅助线构造![]() ,由圆的半径相等、
,由圆的半径相等、![]() 与圆相切及特殊角,利用等量代换将所求线段转化为已知线段求解;
与圆相切及特殊角,利用等量代换将所求线段转化为已知线段求解;
(2)猜想![]() 与
与![]() 相切,但未知切点,常用方法为作垂线,证半径,结合直角三角形中
相切,但未知切点,常用方法为作垂线,证半径,结合直角三角形中![]() 角所对的边等于斜边的一半求解;
角所对的边等于斜边的一半求解;
(3)线段之间的函数关系式,一般为一次函数,分三种情况讨论:点![]() 在
在![]() 左侧;点
左侧;点![]() 在
在![]() 上;点
上;点![]() 在
在![]() 右侧三种情况,构造直角三角形,利用三角函数及切线性质求解.
右侧三种情况,构造直角三角形,利用三角函数及切线性质求解.
解:(1)连接![]() ,
,![]() ,如解图①,
,如解图①,![]() ,
,![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() 为等边三角形,∴
为等边三角形,∴![]() .
.
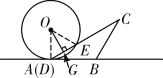
图①
(2)![]() 与
与![]() 相切;
相切;
理由如下:过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,如解图②,
,如解图②,
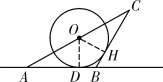
图②
∵![]() 与
与![]() 相切于点
相切于点![]() ,∴
,∴![]() ,
,
在![]() 中,
中,![]() ,∴
,∴![]() ,
,
又∵![]() ,∴
,∴![]() ,在
,在![]() 中,
中,![]() ,
,
∴![]() ,在
,在![]() 中,
中,![]() ,
,
∴![]() ,即
,即![]() 为
为![]() 的半径,∴
的半径,∴![]() 与
与![]() 相切;
相切;
(3)当点![]() 在
在![]() 上时,
上时,![]() ,
,![]() ;
;
当点![]() 在点
在点![]() 左侧时,连接
左侧时,连接![]() 交
交![]() 于点
于点![]() ,如解图③,
,如解图③,
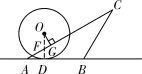
图③
∵![]() 与
与![]() 相切于点
相切于点![]() ,∴
,∴![]() ,
,
又∵![]() ,∴
,∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴在![]() 中,
中,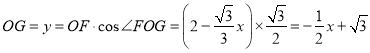 ,
,
此时![]() 的取值范围是:
的取值范围是:![]() ;
;
当点![]() 在点
在点![]() 的右侧时,连接
的右侧时,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,如解图④,
,如解图④,
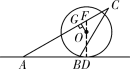
图④
同理可得:![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
在![]() 中,
中,
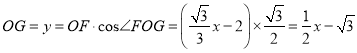 ,
,
此时![]() 的取值范围是:
的取值范围是:![]() .
.
综上,![]() 与
与![]() 之间的函数关系式为
之间的函数关系式为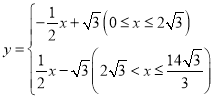 .
.

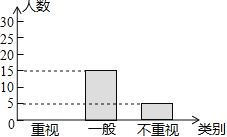
【题目】某教研机构为了了解初中生课外阅读名著的现状,随机抽取了某校50名初中生进行调查,依据相关数据绘制成了以下不完整的统计图,请根据图中信息解答下列问题:
类别 | 重视 | 一般 | 不重视 |
人数 | a | 15 | b |
(1)求表格中a,b的值;
(2)请补全统计图;
(3)若某校共有初中生2000名,请估计该校“重视课外阅读名著”的初中生人数.