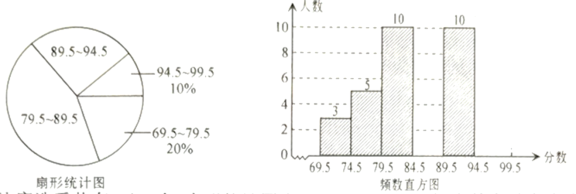
题目内容
【题目】如图,某市有一块长为![]() 米,宽为
米,宽为![]() 米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像,左右两边修两条宽为
米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像,左右两边修两条宽为![]() 米的道路.(
米的道路.(![]() ).
).
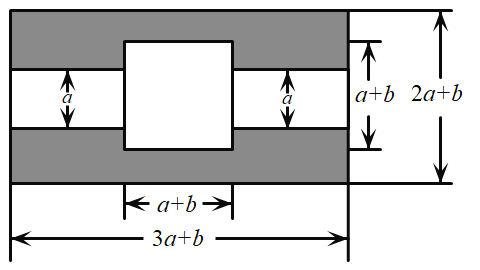
(1)①试用含![]() 的代数式表示绿化的面积是多少平方米?
的代数式表示绿化的面积是多少平方米?
②假设阴影部分可以拼成一个矩形.请你求出所拼矩形相邻两边的长:如果要使所拼矩形面积最大,求![]() 与
与![]() 满足的关系式;
满足的关系式;
(2)若![]() ,请求出绿化面积.
,请求出绿化面积.
【答案】(1)①绿化面积![]() ;②当矩形面积最大时
;②当矩形面积最大时![]() ;(2)绿化面积为45平方米.
;(2)绿化面积为45平方米.
【解析】
(1)①根据绿化面积等于总面积减去中间空白图形的面积列出代数式化简即可;
②绿化面积![]() 因式分解后,讨论两条邻边相等即可求得
因式分解后,讨论两条邻边相等即可求得![]() 与
与![]() 满足的关系式;
满足的关系式;
(2)代入a、b的值后即可求得绿化面积.
解:(1)①绿化面积![]()
![]() ,
,
![]()
![]() ;
;
②由题意可知:矩形面积![]()
![]() .
.
∴矩形相邻两边的长为![]() 和
和![]() ,
,
当矩形面积最大时![]() ,
,
即![]() ;
;
若![]() ,
,
此时,![]() ,
,
![]() ,
,
不符合![]() ,故舍去,
,故舍去,
综上,当矩形面积最大时,![]() ;
;
(2)当![]() 时,
时,
绿化面积![]()
![]()
![]()
答:绿化面积为45平方米.

练习册系列答案
相关题目