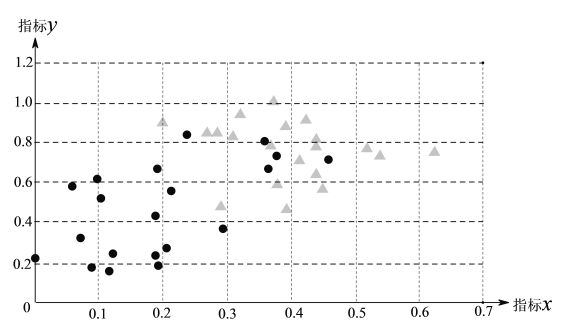
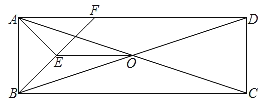
题目内容
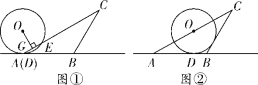
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为直径作⊙
为直径作⊙![]() ,在⊙
,在⊙![]() 上一点
上一点![]() ,
,![]() .
.

(1)求证:![]() 是⊙
是⊙![]() 的切线;
的切线;
(2)过![]() 作
作![]() 分别与
分别与![]() 、
、![]() 和⊙
和⊙![]() 交于点
交于点![]() 、
、![]() 、
、![]() ,若
,若![]() ,
,![]() .
.
①求⊙![]() 的半径长;
的半径长;
②直接写出![]() 的长.
的长.
【答案】(1)见解析;(2)①![]() ;②
;②![]() .
.
【解析】
(1)连接![]() 、
、![]() ,由
,由![]() ,
,![]() ,可得
,可得![]() ,
,![]() ,又
,又![]() 为切线,可知
为切线,可知![]() ,可得
,可得![]() 为切线;
为切线;
(2)①![]() ,
,![]() 解三角形可得
解三角形可得![]() ,
,![]() ,由
,由![]() ,可得
,可得![]() ,根据垂径定理可知
,根据垂径定理可知![]() ,从而可得
,从而可得![]() ,
,![]() ,所以半径为5,
,所以半径为5,
②先证明![]() ,由正切值为
,由正切值为![]() 求出AC=8,进而得
求出AC=8,进而得![]() ,即可知
,即可知![]() .
.
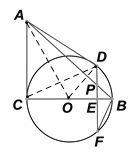
(1)证明:如图,连接![]() 、
、![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
即![]() ,
,
![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 的切线,
的切线,
![]() ,
,
![]() ,
,
![]() 为
为![]() 的切线;
的切线;
(2)解:①∵在![]() 中,
中,![]() .
.
∴![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
又![]() 是
是![]() 的直径,
的直径,![]() ,
,
∴![]() ,
,
∴![]()
⊙![]() 的半径长
的半径长![]() ,
,
②![]() ,
,
求解如下:连接AO,
∵![]() 、
、![]() 是圆的切线,
是圆的切线,
![]()
![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]() ,即:
,即:![]()
![]() ,
,
∴![]() ,即
,即![]() ,
,
∵![]()
∴![]() ;
;
又∴![]() ,
,
∴![]() .
.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目