题目内容
19.(1)已知一元二次方程x2-4x+m=0有唯一实数根,求($\frac{1}{m+2}$-$\frac{1}{m-2}$)÷$\frac{m}{{m}^{2}-4}$的值;(2)小明是这样完成“作∠MON的平分线”这项作业的:
“如图,①以O为圆心,任意长为半径画弧,分别交OM,ON于点A,B;②分别作线段OA,OB的垂直平分线l1,l2(垂足分别记为C,D),记l1与l2的交点为P;③作射线OP,则射线OP为∠MON的平分线.”
你认为小明的作法正确吗?如果正确,请你给证明,如果不正确,请指出错在哪里.
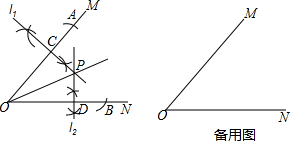
分析 (1)首先利用根的判别式得出m的值,进而化简分式求出即可;
(2)利用全等三角形的判定方法得出Rt△PCO≌Rt△PDO(HL),进而得出射线OP是∠MON的平分线.
解答 解:(1)∵一元二次方程x2-4x+m=0有唯一实数根,
∴(-4)2-4×1×m=0,
∴m=4,
($\frac{1}{m+2}$-$\frac{1}{m-2}$)÷$\frac{m}{{m}^{2}-4}$
=$\frac{-4}{(m+2)(m-2)}$×$\frac{(m-2)(m+2)}{m}$
=-$\frac{4}{m}$,
将m=4代入原式得:原式=-1;
(2)小明的作法正确.
理由:由作法知:OA=OB,
又∵l1,l2垂分别是OA,OB的垂直平分线,垂足分别是C,D,
∴OC=OD,∠PCO=∠PDO=90°,
在Rt△PCO和Rt△PDO中
∵$\left\{\begin{array}{l}{OC=OD}\\{OP=OP}\end{array}\right.$,
∴Rt△PCO≌Rt△PDO(HL),
∴∠POC=∠POD,
即射线OP是∠MON的平分线.
点评 此题主要考查了基本作图以及分式的化简求值和全等三角形的判定与性质等知识,正确得出Rt△PCO≌Rt△PDO是解题关键.

练习册系列答案
相关题目
7.下列运算正确的是( )
| A. | $\sqrt{(-9)×(-4)}=\sqrt{-9}×\sqrt{-4}=6$ | B. | $\sqrt{(-3)^{2}}$=-3 | C. | ($\sqrt{3}$)2=3 | D. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ |
4.-3的倒数是( )
| A. | -3 | B. | 3 | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
 如图,⊙M和⊙N都与x轴和y轴相切,圆心A与圆心B都在反比例函数y=$\frac{-1}{x}$的图象上,则图中阴影部分面积等于π.
如图,⊙M和⊙N都与x轴和y轴相切,圆心A与圆心B都在反比例函数y=$\frac{-1}{x}$的图象上,则图中阴影部分面积等于π.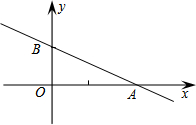 如图,在以点O为原点的直角坐标系中,一次函数y=-$\frac{1}{2}$x+1的图象与x轴交于A,与y轴交于点B,点C在第二象限内且为直线AB上一点,OC=$\frac{1}{2}$AB,反比例函数y=$\frac{k}{x}$的图象经过点C,则k的值为-$\frac{11}{50}$.
如图,在以点O为原点的直角坐标系中,一次函数y=-$\frac{1}{2}$x+1的图象与x轴交于A,与y轴交于点B,点C在第二象限内且为直线AB上一点,OC=$\frac{1}{2}$AB,反比例函数y=$\frac{k}{x}$的图象经过点C,则k的值为-$\frac{11}{50}$.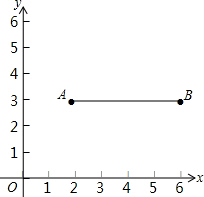 如图,在平面直角坐标系中,已知点A(2,3)、B(6,3),连结AB.若对于平面内一点P,线段AB上都存在点Q,使得PQ≤1,则称点P是线段AB的“邻近点”.
如图,在平面直角坐标系中,已知点A(2,3)、B(6,3),连结AB.若对于平面内一点P,线段AB上都存在点Q,使得PQ≤1,则称点P是线段AB的“邻近点”.