��Ŀ����
8����ͼͼ1����ABC�У�AB=AC����BAC=90�㣬AE�ǹ�A���һ��ֱ�ߣ���B��C��DE����࣬BD��AE��D��CE��AE��E��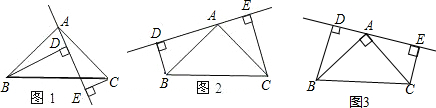
��1����ABD���CAEȫ����BD��DE+CE�������˵�����ɣ�
��2����ͼͼ2����ֱ��AE�Ƶ�A��ת��ͼ2��ʾ��λ�ã�BD��CE��ʱ�������������䣬��BD��DE��CE�Ĺ�ϵ��Σ���ֻ��ش���ۣ���
��3����ͼͼ3����ֱ��AE�Ƶ�A��ת��ͼ3��ʾ��λ�ã�BD��CE��ʱ�������������䣬��BD��DE��CE�Ĺ�ϵ��Σ���ֻ��ش���ۣ���
���� ��1��������֪������֤�á�BAD=��ACE���Ҹ���ȫ�������ε��ж���֤����ABD�ա�CAE�����ݸ��߶εĹ�ϵ���ɵý��ۣ�
��2��BD=DE+CE������ȫ�������ε��ж���֤����ABD�ա�CAE�����ݸ��߶εĹ�ϵ���ɵý��ۣ�
��3��ͬ������BD=DE+CE�Գ�����
��� �⣺֤�����£�
��1���ߡ�BAC=90�㣬���BAD+��CAE=90�㣬
��CE��AE�����ACE+��CAE=90�㣬
���ACE=��BAD��
�֡�BD��AE��CE��AE��
���ADB=��CEA=90�㣬
�ڡ�ABD�͡�CAE�У�
$\left\{\begin{array}{l}{��ADB=��CEA}\\{��ACE=��BAD}\\{AB=AC}\end{array}\right.$��
���ABD�ա�CAE��AAS����
��BD=AE��AD=CE��
��AE=DE+AD��
��BD=DE+CE��
��2��DE=BD+CE��
�ߡ�BAC=90�㣬���BAD+��CAE=90�㣬
��CE��AE�����ACE+��CAE=90�㣬
���ACE=��BAD��
�֡�BD��AE��CE��AE
���ADB=��CEA=90�㣬
�ڡ�ABD�͡�CAE�У�
$\left\{\begin{array}{l}{��ADB=��CEA}\\{��ACE=��BAD}\\{AB=AC}\end{array}\right.$��
���ABD�ա�CAE��AAS����
��BD=AE��AD=CE��
��DE=AE+AD��
��DE=BD+CE��
��3�������ǣ���B��C��AE����ʱ��BD=DE+CE����B��C��AEͬ��ʱ��BD=DE-CE��DE=BD+CE��
���� ���⿼����ȫ�������ε��ж������ʣ��漰��ֱ�������ε����ʡ���ǺͲ��ǵ����ʵ�֪ʶ�㣬��������ȫ�������ε��ж������ǽ���Ĺؼ���

| A�� | x2•x4=x6 | B�� | x2+x3=x5 | C�� | ��x2��3=x5 | D�� | x10��x2=x5 |
| A�� | $\frac{1}{2}$ | B�� | $\frac{\sqrt{2}}{2}$ | C�� | $\frac{\sqrt{3}}{2}$ | D�� | 1 |
| A�� | ������ | B�� | ʼ�յ���16 | C�� | ʼ�յ���4 | D�� | ����ȷ�� |
 ��ͼ��һ���߳�Ϊ20cm�������Σ������ĶԽ���AC�ֳ���Σ���ÿһС��Ϊ�Խ����������Σ��������С�������ܳ����ܺ�Ϊ80cm��
��ͼ��һ���߳�Ϊ20cm�������Σ������ĶԽ���AC�ֳ���Σ���ÿһС��Ϊ�Խ����������Σ��������С�������ܳ����ܺ�Ϊ80cm��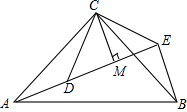 ��ͼ����ACB�͡�DCE��Ϊ���������Σ���ACB=��DCE=90�㣬��A��D��E��ͬһֱ���ϣ�CMΪ��DCE��DE���ϵĸߣ�����BE��
��ͼ����ACB�͡�DCE��Ϊ���������Σ���ACB=��DCE=90�㣬��A��D��E��ͬһֱ���ϣ�CMΪ��DCE��DE���ϵĸߣ�����BE�� ��ͼ��ֱ��l1��l2��l3��ֱ�������ε���������A��B��C�ֱ���l1��l2��l3�ϣ��ҡ�ABC=90�㣮����1=65�㣬���2=25�㣮
��ͼ��ֱ��l1��l2��l3��ֱ�������ε���������A��B��C�ֱ���l1��l2��l3�ϣ��ҡ�ABC=90�㣮����1=65�㣬���2=25�㣮