题目内容
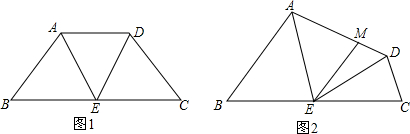
19. 如图,△ACB和△DCE均为等腰三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.
如图,△ACB和△DCE均为等腰三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.(1)求∠AEB的度数;
(2)线段CM、AE、BE之间存在怎样的数量关系?请说明理由.
分析 (1)首先证明△ACD≌△BCE,得出∠ADC=∠BEC,由△DCE为等腰直角三角形,得到∠CDE=∠CED=45°,因为点A,D,E在同一直线上,得到∠ADC=135°,∠BEC=135°,于是得到∠AEB=∠BEC-∠CED=90°;
(2)由∠DCE=90°,CD=CE,CM⊥DE,可得CM=DM=EM,所以DE=DM+EM=2CM,据此判断出AE=BE+2CM即可
解答 解:(1)∵△ACB和△DCE均为等腰直角三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=90°.
∴∠ACD=∠BCE.
在△ACD和△BCE中,
$\left\{\begin{array}{l}{CA=BC}\\{∠ACD=∠BDE}\\{CD=CE}\end{array}\right.$,
∴△ACD≌△BCE(SAS).
∴∠ADC=∠BEC,AD=BE.
∵△DCE为等腰直角三角形,
∴∠CED=∠CDE=45°.
∵点A,D,E在同一直线上,
∴∠ADC=135°.
∴∠BEC=135°.
∴∠AEB=∠BEC-∠CED=135°-45°=90°.
(2)AE=BE+2CM.
理由:
∵CD=CE,CM⊥DE,
∴DM=ME.
∵∠DCE=90°,
∴DM=ME=CM.
∴AE=AD+DE=BE+2CM.
点评 此题主要考查了全等三角形的判定方法和性质以及等腰三角形的性质,要熟练掌握,解答此题的关键是要明确:在判定三角形全等时,关键是选择恰当的判定条件.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
10. 问题:我们已经知道反比例函数的图象是双曲线,那么函数y=$\frac{6}{|x|-3}$的图象是怎样的呢?
问题:我们已经知道反比例函数的图象是双曲线,那么函数y=$\frac{6}{|x|-3}$的图象是怎样的呢?
经验:
(1)我们在研究反比例函数的图象和性质的时候是从以下两个方面来探究的:
①由数想到形----先根据表达式中x、y的数量关系,初步估计图象的基本概貌.如:形状(直线或曲线);位置(所在区域、与直线或坐标轴的交点情况);趋势(上升、下降);对称性等.
②描点画图----根据已有的函数画图的经验,利用描点画图.
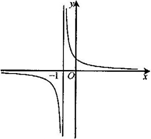
(2)我们知道,函数y=$\frac{2}{x+1}$的图象是如图所示的两条曲线,一支在过点(-1,0)且平行于y轴的直线的右侧且在x轴的上方,另一支在过点(-1,0)且平行于y轴的直线的左侧且在x轴的下方.
探索:请你根据以上经验,研究函数y=$\frac{6}{|x|-3}$的图象和性质并解决相关问题.
(1)由数想形:
(2)描点画图:
①列表:
②画图: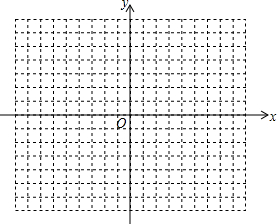
应用:观察你所画的函数图象,解答下列问题:
(3)若点A(a,c),B(b,c)为该函数图象上不同的两点,则a+b=0;
(4)直接写出当$\frac{6}{|x|-3}$≥-2时x的取值范围.
 问题:我们已经知道反比例函数的图象是双曲线,那么函数y=$\frac{6}{|x|-3}$的图象是怎样的呢?
问题:我们已经知道反比例函数的图象是双曲线,那么函数y=$\frac{6}{|x|-3}$的图象是怎样的呢?经验:
(1)我们在研究反比例函数的图象和性质的时候是从以下两个方面来探究的:
①由数想到形----先根据表达式中x、y的数量关系,初步估计图象的基本概貌.如:形状(直线或曲线);位置(所在区域、与直线或坐标轴的交点情况);趋势(上升、下降);对称性等.
②描点画图----根据已有的函数画图的经验,利用描点画图.
(2)我们知道,函数y=$\frac{2}{x+1}$的图象是如图所示的两条曲线,一支在过点(-1,0)且平行于y轴的直线的右侧且在x轴的上方,另一支在过点(-1,0)且平行于y轴的直线的左侧且在x轴的下方.
探索:请你根据以上经验,研究函数y=$\frac{6}{|x|-3}$的图象和性质并解决相关问题.
(1)由数想形:
(2)描点画图:
①列表:
| x | … | … | |||||||||||||||
| y | … | … |

应用:观察你所画的函数图象,解答下列问题:
(3)若点A(a,c),B(b,c)为该函数图象上不同的两点,则a+b=0;
(4)直接写出当$\frac{6}{|x|-3}$≥-2时x的取值范围.
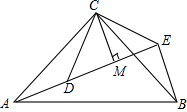
4.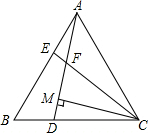 如图,在等边△ABC中,点D,E分别在边BC,AB上,且BD=AE,AD与CE交于点F,作CM⊥AD,垂足为M,下列结论不正确的是( )
如图,在等边△ABC中,点D,E分别在边BC,AB上,且BD=AE,AD与CE交于点F,作CM⊥AD,垂足为M,下列结论不正确的是( )
 如图,在等边△ABC中,点D,E分别在边BC,AB上,且BD=AE,AD与CE交于点F,作CM⊥AD,垂足为M,下列结论不正确的是( )
如图,在等边△ABC中,点D,E分别在边BC,AB上,且BD=AE,AD与CE交于点F,作CM⊥AD,垂足为M,下列结论不正确的是( )| A. | AD=CE | B. | MF=$\frac{1}{2}$CF | C. | ∠BEC=∠CDA | D. | AM=CM |
 如图,在平面直角坐标系中,直线AB与x轴、y轴的正半轴分别交于点A,B,直线CD与x轴正半轴、y轴负半轴分别交于点D,C,AB与CD相交于点E,点A,B,C,D的坐标分别为(8,0)、(0,6)、(0,-3)、(4,0),点M是OB的中点,点P在直线AB上,过点P作PQ∥y轴,交直线CD于点Q,设点P的横坐标为m.
如图,在平面直角坐标系中,直线AB与x轴、y轴的正半轴分别交于点A,B,直线CD与x轴正半轴、y轴负半轴分别交于点D,C,AB与CD相交于点E,点A,B,C,D的坐标分别为(8,0)、(0,6)、(0,-3)、(4,0),点M是OB的中点,点P在直线AB上,过点P作PQ∥y轴,交直线CD于点Q,设点P的横坐标为m.