题目内容
12. △AOB在平面直角坐标系中的位置如图所示,其中,A(0,-3),B(-2,0),O是坐标原点.
△AOB在平面直角坐标系中的位置如图所示,其中,A(0,-3),B(-2,0),O是坐标原点.(1)将△AOB先作其关于x轴的对称图形,再把新图形向右平移3个单位,在图中画出两次变换后所得的图形△AO1B1;
(2)若点M(x,y)在△AOB上,则它随上述两次变换后得到点M1,则点M1的坐标是(x+3,-y).
分析 (1)首先确定A、B、C三点关于x轴的对称点位置,再向右平移3个单位找到对应点位置,然后再连接即可;
(2)根据关于x轴对称的点的坐标特点:横坐标不变,纵坐标相反可得点M(x,y)关于x轴的对称图形上的点的坐标为(x,-y),再向右平移3个单位,点的横坐标+3,纵坐标不变.
解答  解:(1)如图所示:
解:(1)如图所示:
(2)点M(x,y)关于x轴的对称图形上的点的坐标为(x,-y),再向右平移3个单位得到点M1的坐标是(x+3,-y).
故答案为:(x+3,-y).
点评 此题主要考查了作图--平移变换和轴对称变换,关键是掌握点的坐标的变化规律.

练习册系列答案
相关题目
4. 已知:如图,在菱形ABCD中,F为边AB的中点,DF与对角线AC交于点G,过G作GE⊥AD于点E,若AB=2,且∠1=∠2,则下列结论不正确的是( )
已知:如图,在菱形ABCD中,F为边AB的中点,DF与对角线AC交于点G,过G作GE⊥AD于点E,若AB=2,且∠1=∠2,则下列结论不正确的是( )
 已知:如图,在菱形ABCD中,F为边AB的中点,DF与对角线AC交于点G,过G作GE⊥AD于点E,若AB=2,且∠1=∠2,则下列结论不正确的是( )
已知:如图,在菱形ABCD中,F为边AB的中点,DF与对角线AC交于点G,过G作GE⊥AD于点E,若AB=2,且∠1=∠2,则下列结论不正确的是( )| A. | DF⊥AB | B. | CG=2GA | C. | CG=DF+GE | D. | S四边形BFGC=$\sqrt{3}$-1 |
1.若用a、b表示2+$\sqrt{5}$的整数部分和小数部分,则a、b可表示为( )
| A. | 4和$\sqrt{5}$-2 | B. | 3和$\sqrt{5}$-3 | C. | 2和$\sqrt{5}$-2 | D. | 5和$\sqrt{5}$-5 |
 如图,l∥m,等边△ABC的顶点A在直线m上,CB的延长线交m于点D,则∠α=20°.
如图,l∥m,等边△ABC的顶点A在直线m上,CB的延长线交m于点D,则∠α=20°.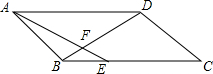 如图,E是平行四边形ABCD的边BC上一点,且$\frac{BE}{EC}$=$\frac{1}{2}$,对角线BD与AE相交于F,已知S△BEF=2,则S△ABD=24.
如图,E是平行四边形ABCD的边BC上一点,且$\frac{BE}{EC}$=$\frac{1}{2}$,对角线BD与AE相交于F,已知S△BEF=2,则S△ABD=24.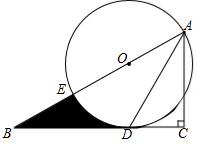 如图,在Rt△ABC中,∠C=90°,AD是△ABC的角平分线,圆心在AB上,以AD为弦的⊙O交AB于点E.
如图,在Rt△ABC中,∠C=90°,AD是△ABC的角平分线,圆心在AB上,以AD为弦的⊙O交AB于点E.