题目内容
5．
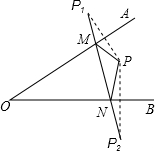如图：点P为∠AOB内一点，分别作出P点关于OA、OB的对称点P1，P2，连接P1P2交OA于M，交OB于N，P1P2=22，则△PMN的周长为22．
分析 根据轴对称的性质可得出PM=P1M、PN=P2N，再利用三角形的周长公式结合线段P1P2的长度即可得出结论．
解答 解：∵点P1、P2分别为P点关于OA、OB的对称点，
∴PM=P1M，PN=P2N，
∴C△PMN=PM+MN+PN=P1M+MN+P2N=P1P2=22．
故答案为：22．
点评 本题考查了轴对称的性质，根据轴对称的性质找出C△PMN=P1P2是解题的关键．
练习册系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
15．给出下列各数：0，π，-$\frac{22}{7}$，3.14，-10，其中有理数的个数是（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
16．下列图形中，是中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
13．已知直角三角形的一个锐角为60度，斜边长为2，那么此直角三角形的周长是（ ）
| A． | 2.5 | B． | 3 | C． | $\sqrt{3}$+2 | D． | $\sqrt{3}$+3 |
10．若关于x的一元二次方程ax2+bx+5=0（a≠0）的解是x=1，则2012-a-b的值是（ ）
| A． | 2020 | B． | 2018 | C． | 2017 | D． | 2016 |
17．直线AB上有一点异于A、B的C，直线AB外有一点D，则A、B、C、D四点能确定的直线有（ ）
| A． | 3条 | B． | 4条 | C． | 1条或4条 | D． | 4条或6条 |
14．下列函数中，y随x的增大而减小的有（ ）
| A． | y=-3x+1 | B． | y=2x-1 | C． | y=x-1 | D． | y=$\frac{1}{5}$x-5 |