题目内容
 如图,S△AFG=5a,S△ACG=4a,S△BFG=7a,则S△AEG=( )
如图,S△AFG=5a,S△ACG=4a,S△BFG=7a,则S△AEG=( )A、
| ||
B、
| ||
C、
| ||
D、
|
分析:首先由已知根据等高的三角形的面积之比等于边之比得到:
=
,求出S△BCG,同理可得
=
,
变换得到
=
=
,代入S△ACG=4a即可求出选项.
| S△AFG |
| S△ACG |
| 5 |
| 4 |
| S△BFG |
| S△BCG |
| S△ABG |
| S△AEG |
| S△BCG |
| S△CEG |
变换得到
| S△AEG |
| S△CEG |
| S△ABG |
| S△BCG |
| 15 |
| 7 |
解答:解:△AFG的边FG上和△ACG的边CG上的高相同,S△AFG=5a,S△ACG=4a,
由三角形的面积公式得:
=
=
,
同理
=
=
,
∵S△BFG=7a,
可得;S△BCG=
a,
∵△ABG的边BG上和△AEG的边EG上的高相同,
∴
=
,
同理
=
,
∴
=
,
即:
=
=
=
,
∵S△ACG=4a,
∴S△AEG=
a.
故选D.
由三角形的面积公式得:
| S△AFG |
| S△ACG |
| 5a |
| 4a |
| 5 |
| 4 |
同理
| S△BFG |
| S△BCG |
| FG |
| CG |
| 5 |
| 4 |
∵S△BFG=7a,
可得;S△BCG=
| 28 |
| 5 |
∵△ABG的边BG上和△AEG的边EG上的高相同,
∴
| S△ABG |
| S△AEG |
| BG |
| GE |
同理
| S△BCG |
| S△CEG |
| BG |
| GE |
∴
| S△ABG |
| S△AEG |
| S△BCG |
| S△CEG |
即:
| S△AEG |
| S△CEG |
| S△ABG |
| S△BCG |
| 12a | ||
|
| 15 |
| 7 |
∵S△ACG=4a,
∴S△AEG=
| 30 |
| 11 |
故选D.
点评:本题主要考查了面积及等积变换,三角形的面积公式等知识点,巧妙地利用同底等高的面积之比等于边长之比是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
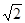 ,若∆ABC固定不动,∆AFG绕点A旋转,AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合),设BE=m,CD=n
,若∆ABC固定不动,∆AFG绕点A旋转,AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合),设BE=m,CD=n
 ;
; 如图,S△AFG=5a,S△ACG=4a,S△BFG=7a,则S△AEG=
如图,S△AFG=5a,S△ACG=4a,S△BFG=7a,则S△AEG= a
a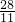 a
a a
a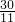 a
a

 a
a a
a a
a a
a