题目内容
20.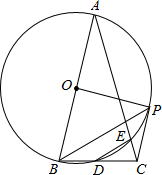 如图,在△ABC中,AB=AC,∠A=30°,以AB为直径的⊙O交BC于点D,交AC于点E,过点B作∠DBP=30°,交⊙O于点P,连接DE、CP、OP.
如图,在△ABC中,AB=AC,∠A=30°,以AB为直径的⊙O交BC于点D,交AC于点E,过点B作∠DBP=30°,交⊙O于点P,连接DE、CP、OP.(1)BD与DC的数量关系是相等,DE与BP的位置关系是平行;
(2)求∠BOP的度数;
(3)求证:CP是⊙O的切线.
分析 (1)连结AD,如图1,根据圆周角定理,由AB为⊙O的直径得到∠ADB=90°,则根据等腰三角形的性质可得BD=DC;再利用三角形内角和计算出∠ABC=∠ACB=75°,根据圆内接四边形的性质得∠DEC=∠ABC=75°,于是可计算出∠EDC=30°,所以∠EDC=∠DBP=30°,则根据平行线的判定方法即可得到DE∥BP.
(2)由∠DBP=30°,∠ABC=75°得∠OBP=45°,则利用OB=OP得到∠OPB=∠OBP=45°,所以∠BOP=90°;
(3)作CH⊥AB于H,如图,在Rt△AHC中根据含30度的直角三角形三边的关系得到CH=$\frac{1}{2}$AC,则CH=$\frac{1}{2}$AB=OP,再证明四边形OPCH为矩形得到∠OPC=90°,然后根据切线的判定定理得到CP是⊙O的切线.
解答 (1)解:连结AD,如图1,
∵AB为⊙O的直径,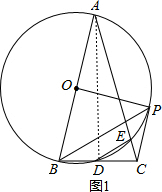
∴∠ADB=90°,
∴AD⊥BC,
∵AB=AC,
∴BD=DC;
∵AB=AC,∠A=30°,
∴∠ABC=∠ACB=75°,
而∠DEC=∠ABC=75°,
∴∠EDC=180°-∠DEC-∠DCE=30°,
∴∠EDC=∠DBP=30°,
∴DE∥BP.
故答案为相等,平行;
(2)解:∵∠DBP=30°,∠ABC=75°,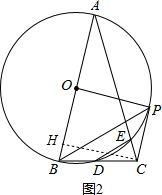
∴∠OBP=45°,
∵OB=OP,
∴∠OPB=∠OBP=45°,
∴∠BOP=90°;
(3)证明:作CH⊥AB于H,如图,
在Rt△AHC中,∵∠HAC=30°,
∴CH=$\frac{1}{2}$AC,
而AC=AB,
∴CH=$\frac{1}{2}$AB,
∴CH=OP,
∵∠POH=90°,CH⊥OH,
∴OP∥CH,
∴四边形OPCH为平行四边形,
而∠POH=90°,
∴四边形OPCH为矩形,
∴∠OPC=90°,
∴OP⊥PC,
∴CP是⊙O的切线.
点评 本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了等腰三角形的性质.

 阅读快车系列答案
阅读快车系列答案 如图,若O为EH的中点,要使△EOF≌△HOG,不能加什么条件( )
如图,若O为EH的中点,要使△EOF≌△HOG,不能加什么条件( )| A. | FO=GO | B. | AB∥CD | C. | ∠AFG=∠FGD | D. | EF=GH |
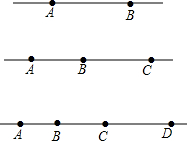 在一条直线上取两点A,B共得几条线段?在一条直线上取三个点A,B,C,共得几条线段?在一条直线上取A,B,C,D四个点时,共得多少条线段?在一条直线上取n个点时,共可得多少条线段?若将此题中直线上由点变为线段,结论有何变化?
在一条直线上取两点A,B共得几条线段?在一条直线上取三个点A,B,C,共得几条线段?在一条直线上取A,B,C,D四个点时,共得多少条线段?在一条直线上取n个点时,共可得多少条线段?若将此题中直线上由点变为线段,结论有何变化? 如图,在△ABC中,AB=AC,以AB为直径的半圆⊙O交BC于点D,DE⊥AC,垂足为点E.
如图,在△ABC中,AB=AC,以AB为直径的半圆⊙O交BC于点D,DE⊥AC,垂足为点E.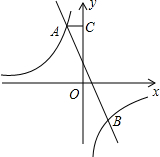 如图,已知双曲线y=$\frac{k}{x}$和直线y=mx+n交于点A和B,B点的坐标是(2,-3),AC垂直y轴于点C,AC=$\frac{3}{2}$;
如图,已知双曲线y=$\frac{k}{x}$和直线y=mx+n交于点A和B,B点的坐标是(2,-3),AC垂直y轴于点C,AC=$\frac{3}{2}$;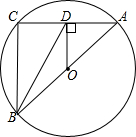 如图,AB是⊙O的直径,AC是⊙O的弦,作0D⊥AC,垂足为点D,连接BD.若AB=5cm,AC=4cm,则BD的长为$\sqrt{13}$.
如图,AB是⊙O的直径,AC是⊙O的弦,作0D⊥AC,垂足为点D,连接BD.若AB=5cm,AC=4cm,则BD的长为$\sqrt{13}$.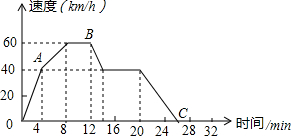 如图,根据汽车行驶情况的图象回答下列问题:
如图,根据汽车行驶情况的图象回答下列问题: